Apoi, puteți apela procedura de interpolare specificând listele de mai sus cu parametrii săi și, în plus, acceptați x ca variabila de interpolare.
Merită remarcat faptul că rezultatul procedurii interp () este o expresie, nu un operator, așa cum a fost în dezvoltarea procedurii de construire a polinomului Lagrange de interpolare.
O altă metodă populară de interpolare este după cum urmează. La fiecare interval dintre punctele nodale adiacente, funcția interpolată este reprezentată ca un polinom. Dar spre deosebire, să zicem, interpolarea Lagrange, unde același polinom este folosit pentru toate punctele, în acest caz, fiecare polinom are propriul său polinom. Mai mult decât atât funcția de interpolare egalitate la nodurile funcției valorilor tabulare interpolate este suprapus pe primul chiar și derivați starea de continuitate a ordinii, una mai mică decât gradul interpolarea polinoame. Un tip similar de interpolare se numește interpolare spline sau interpolare spline. Cea mai populară este interpolarea cu spline cubice.
În Maple, spline () poate fi folosit pentru a efectua interpolarea spline. Procedura are trei parametri obligatorii. Primele două sunt liste cu puncte nodale și valori funcționale, respectiv. Al treilea parametru specifică variabila de interpolare. Dacă nu este specificat al patrulea parametru opțional, interpolarea va fi efectuată de spline cubice, adică Pentru a "cusca" punctele nodului, folosim polinoamele gradului III. De exemplu, dacă parametrii procedurii specifică liste considerate anterior, tabelați valorile funcției la punctele nodului, obținem acest rezultat.

Al patrulea parametru al procedurii spline () poate fi fie unul dintre cuvintele cheie rezervate din setul liniar, quadratic, cubic, quartic, interpolarea polinomului. Indicația unui număr de la 1 la 4 este echivalentă cu utilizarea opțiunilor de text listate, în funcție de ordine, așa cum au fost prezentate mai sus.
Atenție vă rog!
Ca al patrulea parametru, orice număr întreg pozitiv poate fi specificat, nu numai în intervalul de la 1 la 4. Doar pentru aceste numere există un apel alternativ prin opțiunea de text. De exemplu, prin spline (X, Y, x, 5), puteți interpola funcția discutată mai sus cu polinomii de gradul 5 și așa mai departe.
Interpolarea cu polinoame de gradul patru cu aceeași funcție este după cum urmează.

Expresiile sunt destul de greoaie. Să vedem ce se întâmplă dacă folosim dependențe liniare ca polinoame spline.

În comparație cu cazul anterior, se obține un rezultat mai simplu. Cu toate acestea, simplitatea nu înseamnă întotdeauna eficacitatea. Este ușor să vedem acest lucru dacă construim grafice pentru funcțiile de interpolare obținute prin interpolarea spline de către polinoame de grade diferite.
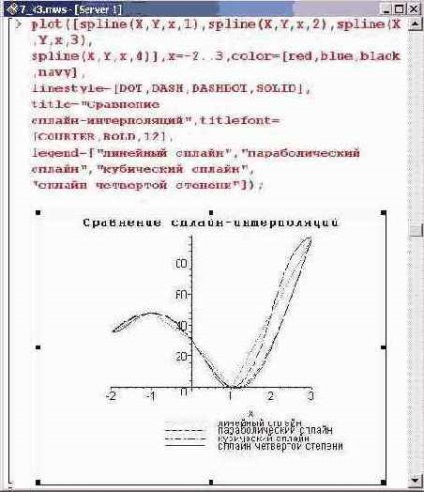
Evident, interpolarea liniară spline este destul de brută. În general, aceasta este pur și simplu o conexiune a punctelor de interpolare cu linii. Acest tip de interpolare este folosit foarte rar. În ceea ce privește utilizarea unor polinoame de alte grade, începând cu al doilea, nu există o diferență distinctă între ele (cel puțin în acest exemplu). Cu toate acestea, nu trebuie să uităm că gradul de polinoame spline determină netezimea curbelor obținute. Acest lucru este deosebit de important în cazurile în care trebuie luate derivate derivate din interpolare. În acest sens, interpolarea polinomică în comparație cu interpolarea spline are avantajul că atât polinomul de interpolare, cât și derivații săi sunt funcții unice continue și netede. Prin urmare, este interesant să se compare rezultatele interpolației polinomiale și interpolarea spline. Pentru a face acest lucru, vom construi grafice ale funcțiilor de interpolare corespunzătoare.
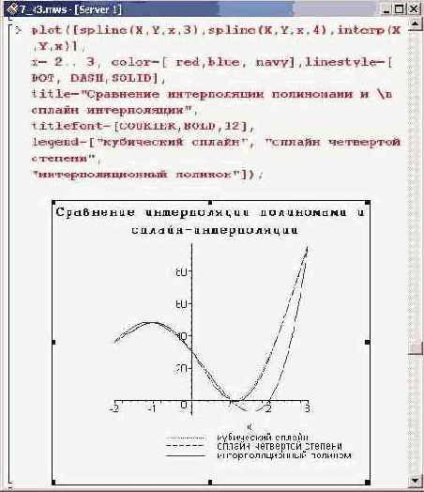
Se poate observa că toate cele trei grafice (spline celui de al treilea și al patrulea și al patrulea grad de gradul polinomului de interpolare) sunt practic aceleași, în special pe partea stângă a figurii. Adevărat, polinomul de interpolare este o funcție mai fină decât primele două. Când etrm cititorul poate întreba de ce polinomul de interpolare de grad egal cu patru, nu coincide cu funcția spline construit pe baza celui de al patrulea polinoame de gradul? Răspunsul trebuie căutat în acele condiții din care se determină funcția spline. Astfel, atunci când interpolarea spline este realizată de polinoame de gradul m în n + 1 puncte, sunt implicate n polinomii spline. În fiecare dintre aceste polinoame este necesar să se determine coeficientul cu m + 1, și astfel obținem n (m + 1) coeficienți necunoscuți. Egalitatea funcției de interpolare la punctul nodului la valorile tabelului conferă n + 1 condiții pentru coeficienții necunoscuți. În plus, nodurile interne (există n-1) Continuitatea se presupune a derivaților de ordinul m-1, inclusiv, care oferă, împreună cu continuitatea funcției, (n-l + (m-l) (n-l)) = m (n-l) condițiile. Astfel, pe condițiile n (m + l) + (n + l)) = (n (m + l) - (m-l)) pe n (m + l) Acest lucru, desigur, nu este suficient - există încă condiții m-1. De regulă, ele sunt obținute prin solicitarea ca numărul corespunzător de derivați continuu de vârf să dispară la limitele regiunii de interpolare. Aceasta este așa-numita alegere naturală a condițiilor suplimentare. În principiu, din punct de vedere matematic, ele pot fi alese în mod arbitrar, în funcție de problema care trebuie rezolvată. În particular, aceste condiții pot fi alese astfel încât atunci când se interpolează cu spline de gradul n, rezultatul este polinomul de interpolare Lagrange.