În practică, de cele mai multe ori este necesar să se poată rezolva problema inversă: care ar trebui să fie erorile absolute ale argumentelor funcției, astfel încât eroarea absolută a funcției să nu depășească o valoare dată.
Să presupunem că este dată valoarea erorii absolute limitative.
Presupunând că toți termenii sunt egali unul cu altul, avem:
În cazul în care eroarea absolută de limitare a tuturor argumentelor este aceeași, atunci:
7.1. Raza bazei cilindrului; înălțimea cilindrului. Cu ce erori absolute avem nevoie pentru a determina R și H astfel încât volumul cilindrului V să poată fi calculat cu până la 0,1 m?
Volumul este calculat prin formula și. Înlocuind toate datele inițiale, obținem aproximativ:
Prin urmare, deoarece n = 3, atunci, folosind formula pentru calculul erorii unei funcții care depinde de trei variabile:
Erori de tabel în valorile funcțiilor elementare.


8. Sarcini pentru activitatea de laborator nr. 1:
8.1. Alocări (independent) Găsiți erorile absolute și relative ale numerelor, dacă au doar cifrele corecte (tabelul variantelor sarcinii).
a) în sens strict; b) într-un sens larg.
Tabel.Probleme pentru desfășurarea muncii independente
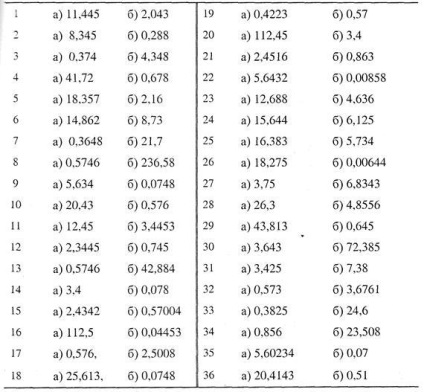
8.2. Sarcină pentru munca independentă. Numărul x (Tabel), toate cifrele din care sunt corecte în sens strict, rotunjesc până la trei cifre semnificative. Pentru rezultatul obținut, se calculează limitele erorilor absolute și relative. În înregistrarea numerelor. indicați numărul de cifre corecte în eroare absolută și relativă.
Tabel.Probleme pentru desfășurarea muncii independente
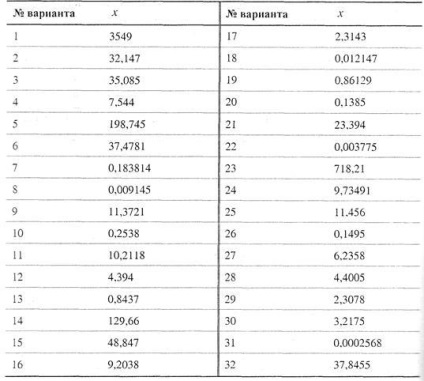
8.3. Calculați valoarea z (tabl) pentru valorile date de a. b și c, folosind o analiză sistematică a erorilor absolute după fiecare operație, precum și folosind metoda limită. Găsiți erorile absolute și relative ale lui z și determinați numărul de cifre corecte în z din ele, dacă numerele a. b și c sunt adevărate în sensul strict.
Tabel. Variante de sarcini pentru desfășurarea muncii independente




8.4. Rezolvați următoarele sarcini folosind metoda limită.
8.4.1. Lungimea rutei aeriene între cele două puncte este de S km. Aeronava depășește această distanță într-un timp t h. Determina limitele vitezei medii a aeronavei dacă: .
8.4.2. Plăcuța electrică este proiectată pentru tensiunea B. Găsiți rezistența spirului electric, dacă se știe că un curent de 5 ± 0,1 A trebuie să treacă prin el.
8.4.3. Bara de cupru are un volum de Vm (). Găsiți masa în cazul în care densitatea cuprului kg / m este.
8.5. Rezolvați următoarele probleme utilizând formula generală de eroare.
8.5.1. Rezistența electrică specifică a unui metal dintr-un fir rotund cu lungimea lm cu o secțiune transversală d mm și rezistența R ohm este determinată de formula :. Find. dacă: l = 12,50 ± 0,01 m, d = 2,00 ± 0,01 mm, R = 0,068 ± 0,0005 Ohm, = 3,141 ± 0,001. Determinați eroarea relativă.
8.5.2. Rezervorul vertical cilindric este umplut cu lichid. Determinați timpul necesar pentru golirea rezervorului printr-o gaură rotundă în partea inferioară. Diametrul Tank D = 1 ± 0,01 m, înălțimea nivelului de lichid H = 2 ± 0,02M, fund cu diametrul găurii d = 0,03 ± 0,001 m, viteza de curgere = 0,6 ± 0,02. Calculul (în secunde) se efectuează conform formulei:
8.6. Rezolvați următoarele probleme folosind problema inversă a teoriei erorilor:
8.6.1. Cu ce precizie este necesar să se măsoare raza cercului R = 30,5 cm și câte cifre semnificative ar trebui să fie limitate la număr. astfel încât zona cercului era cunoscută în limita a 0,1%?
8.6.2. Lungimea laturilor dreptunghiului este egală. . Care este eroarea absolută marginală admisă la măsurarea acestor cantități este aceeași pentru ambele părți, astfel încât zona S a dreptunghiului poate fi determinată cu eroarea absolută limitată?
1. Care sunt erorile absolute și relative?
2. Cum sunt clasificate tipurile de erori?
3. Ce înseamnă cifra în sens strict, larg?
4. Cum este eroarea rotunjită?
5. Cum se determină numărul de cifre corecte prin eroarea relativă a unui număr aproximativ?
6. Cum se propagă erorile absolute și relative în operațiile aritmetice?
7. Cum se evaluează eroarea în valorile funcțiilor elementare?
8. Cum este formulată problema inversă a teoriei erorilor?
9. Care sunt erorile absolute ale argumentelor funcției, astfel încât eroarea absolută a funcției să nu depășească o valoare dată?
Când este metoda de frontieră utilizată?