Studiul primei secțiuni a cursului de geometrie descriptivă se bazează pe utilizarea lui
cunoștințele dobândite de elevi în școală în geometrie. Prin urmare, regulile pentru construirea proiecțiilor de puncte, linii drepte și planuri sunt studiate pe parcursul exemplelor de construire a proiecțiilor de corpuri simple - polyhedra obișnuită.
Un polidron este o parte a spațiului delimitat de o colecție de un număr finit de poligoane plane conectate în așa fel încât fiecare parte a oricărui multi-
gon este partea exactă a unui alt poligon,
NYM. Și în jurul fiecărui vârf există exact un singur ciclu de poligoane. Aceste poligoane sunt numite fețe, liniile de intersecție a fețelor sunt muchii,
Marginile sunt vârfuri ale polyhedronului.
Luați în considerare construirea de imagini de polyhedra. Baza pentru obținerea imaginilor de
În figură, metoda de proiecție dreptunghiulară pe două perechi mutuale,
Perpendicular pe planul de proiecție. Poliedrul are o rudă
dar planurile de proiecție astfel încât numărul maxim de fețe să fie proiectat pe față
planul π 2 fără distorsiuni. Baza este de obicei situată paralel cu
planul zonal al proiecțiilor.
Temele făcute de studenți sunt concepute pentru a preda
puncte, linii drepte și avioane și determină afilierea lor reciprocă pe imaginile prismei și piramidei.
Tema este compusă din următoarele secțiuni:
1. Construcția proiecției prismei și intersecția acesteia cu planul de proiectare.
2. Construcția proiecțiilor piramidei și intersecția acesteia cu planul de proiectare.
Secvența temelor:
1. Construirea proiecțiilor prismei.
2. Intersecția prismei de către planul de proiectare.
3. Construcția proiecțiilor piramidale.
4. Intersecția piramidei cu un plan de proiectare.
5. Construcția secțiunilor.
TL Beloborodova, E.Yu. Kichigina. Proiecții de polyhedra.
Construcția proiecțiilor de prisme
Următoarele semne ne permit să afirmăm că imaginea este o imagine
(sau, în special, un paralelipiped):
- Prezența numai a segmentelor rectilinii, care servesc ca proiecții sau re-
ber, sau fețe; - prezența paralelogramelor sau a dreptunghiurilor ca proiecții ale fețelor laterale;
-prezența oricărui poligon ca proiecție a bazei.
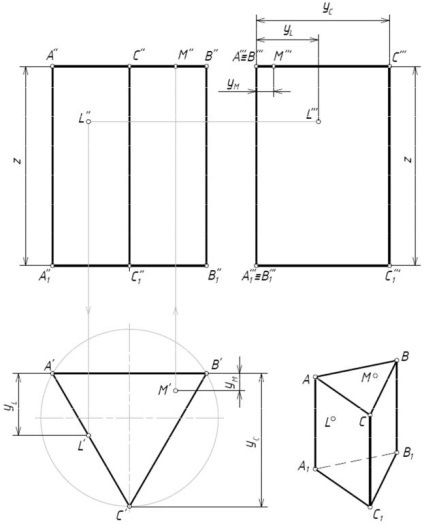
Să construim o imagine a unei prisme triunghiulare regulate (figura 1). Baza premiului este
noi servim triunghiul drept ABC. paralel cu planul orizontal al proiectului.
ții. Prin urmare, pe un plan orizontal, acesta este proiectat într-o dimensiune naturală - proiecția A'B'C '. Deoarece fețele laterale ale prismei sunt planuri orizontale, fiecare parte a triunghiului A'B'C este o proiecție orizontală a feței. Marginile prismei sunt linii drepte proiectate orizontal, astfel încât fiecare vârf al triunghiului A'B'C este o proiecție orizontală a marginii prismei; corespunzător
Marginile AA 1. BB 1, CC 1 sunt proiectate în punctele A ', B', C '.
Construim o proiecție frontală a prismei (vedere frontală). Proiecția frontală este dreptunghiul A''A 1 '' B 1''B ''. Părțile proiecțiilor „A''A„“B 1''B 1 și“ sunt nervuri 1. AA și BB 1. O A''B mână 'și 1''B 1' - proeminențele bazei prismei superioare și inferioare. Proiecția marginii CC 1 - C''C 1 "este situată în interiorul dreptunghiului și coincide cu axa de simetrie. Dreptunghiul A''A 1 '' B 1''B '' este proiecția feței AA 1 B 1 B. Paral-
Proiecția este proiectată pe acest plan fără distorsiuni.
Alte două fețe laterale AA 1 C 1 C și BB 1 C 1 C sunt proiectate cu distorsiuni față de planul frontal π 2.
Construim proiecția profilului prismei folosind coordonatele y și z (figura 1). pro-
proiecția primară a prismei este un dreptunghi A''A 1''C 1''C '' cu nodurile A '' '≡ B' '', A 1 '' '≡ B 1' ''
Cu 1 "'. S ''“. Partea dreptunghiului A''A 1 '' '(B' '' B 1 '' ') este proiecția feței laterale
AA 1 B 1 B și marginile AA 1 și BB 1. aparținând acestei fețe. Fața AA 1 B 1 B este paralelă cu fața
planul π 2 și perpendicular pe planul orizontal π1 și planul profilului
π os 3. Partea S '' 'S' '' 1 - SS proiecție coaste 1. dreptunghi A '' 'A 1' '' S '' 'S' '' este 1, iar proiecția se confruntă cu AA 1 C 1 și C se confruntă cu B 1 CC 1 B. Fața care este AA închis 1 C 1 S. Deoarece ambele fețe nu sunt paralele cu planul profilului proeminențelor, ele sunt proiectate din
zheniyami. Toate marginile laterale ale prismei pe planurile frontale și în profil ale proeminențelor
TL Beloborodova, E.Yu. Kichigina. Proiecții de polyhedra.
Ele sunt proiectate fără distorsiuni, deoarece sunt linii drepte proiectate orizontal.
prin urmare, sunt paralele cu planurile frontale și profilate ale proeminențelor.
TL Beloborodova, E.Yu. Kichigina. Proiecții de polyhedra.
Gasim proiectiile lipsa ale punctelor - L, M.
Punctul L este dat de proiecția frontală L "și aparține feței AA 1 С 1 С.
Pentru a construi o proiecție orizontală a punctului L prin punctul L ', o linie de linii verticale
la intersecția cu linia dreaptă A'C ". în care este proiectată fața AA 1 С 1 С.
coordonarea orizontală cu ajutorul coordonatei y L, găsim proiecția profilului punctului-
L (L ""). Punctul M este dat de proiecția orizontală M 'și aparține bazei superioare
a prismei. Proiecția frontală a punctului M se găsește la intersecția liniei de comunicare verticale trasată prin M '. cu un segment de linie A''B '- proiecția bazei superioare a prismei. Proiecția profilului punctului M (M '' ') se obține cu ajutorul coordonatei lui M.
TL Beloborodova, E.Yu. Kichigina. Proiecții de polyhedra.
Intersecția prismei de către planul de proiectare
Luați în considerare intersecția unei prisme hexagonale obișnuite, proiectând o plană-
Planul γ 1 este înclinat pe axa prismei la un unghi α 1 și perpendicular pe front
avionul. Acest plan intersectează muchiile prismei la punctele A. K și K 1. și cele două fețe ale prismei AK înainte (A'K „A''K«») AK 1 (A'K“ 1. A''K «» 1)
Având în vedere prezența unui plan γ 2. paralel cu π 1. obținem:
- pe planul frontal al proiecțiilor, liniile drepte A''K '' (A''K 1 "), care coincid cu proiecția frontală a planului - γ 1";
- pe plan orizontal - triunghi A'K'K 1 '. ale căror noduri coincid
cu vârfurile hexagonului - proiecția bazei inferioare a prismei;
- pe planul profilului, triunghi A '' 'K' '' K 1 '' '. ale căror noduri sunt construite
folosind linii orizontale de comunicare și coordonate.
Când prisma intersectează planul orizontal γ 2, obținem:
- în planul frontal al proeminențelor - liniile drepte K''M '' (K 1 "M 1") coincid cu proiecția frontală a planului - γ 2 ";
- pe planul orizontal al proiecțiilor - patrulaterală K'M'M 1 'K 1'. ale cărui noduri K 'și K 1' coincid cu vârfurile hexagonului - proiecțiile bazei inferioare a prismei, iar partea M'M 1 'este proiecția orizontală a liniei de intersecție a frontului-
planurile proeminente γ 2 și γ 3 (proiecția frontală a liniei MM-1 este linia punct-
- pe planul profilului proeminențelor, liniile drepte K''K 1 '' '(M "' M 1" ") sunt construite din
puterea liniilor de comunicare orizontale.
Planul γ 3 este înclinat față de axa prismei la un unghi α 2 și perpendicular pe planul frontal.
Planul γ 3 intersectează fețele din față și din spate de-a lungul liniilor drepte MN și M 1 N 1.
Ca urmare a intersecției, obținem:
- în planul frontal al proeminențelor - proeminențele liniilor M''N "(M 1" N 1 ") coincid,
cu proiecția planului γ 3 ';
- pe planul orizontal al proiecțiilor - quadrangle M'N'N 1 'M 1';
TL Beloborodova, E.Yu. Kichigina. Proiecții de polyhedra.
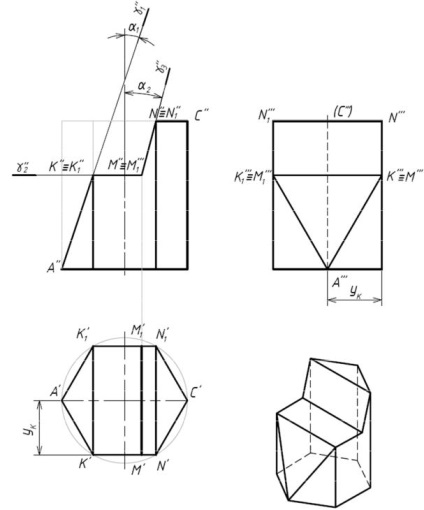
- pe planul profilului proeminențelor - cvadrangul M '' 'N' '' N 1 '' 'M 1' ''.
TL Beloborodova, E.Yu. Kichigina. Proiecții de polyhedra.
Construcția proiecțiilor piramidei
Următoarele semne ne permit să afirmăm că este prezentată piramida:
-Prezența numai a segmentelor rectilinii care servesc ca proiecții de margini sau fețe,
- prezența triunghiurilor ca proiecții ale fețelor laterale; - prezența oricărui poligon ca proiecție a bazei;
-Prezența vârfului piramidei ca punct de intersecție a marginilor laterale.
Construim proiecțiile unei piramide triunghiulare regulate (figura 3). Piramida cheamă -
Xia corectă dacă baza piramidei este un poligon regulat, iar fețele laterale - triunghiuri isoscele egale și baza înălțimea piramidei regulată este centrul descrisă (sau inscripționată) despre circumferința poligonului.
Baza piramidei este compatibilă cu planul orizontal al proiecțiilor, iar în acest plan este proiectat în dimensiune completă. În același timp, înălțimea piramidei de pe munte,
Planul zonal este proiectat într-un punct. Pentru a construi o proiecție orizontală a piramidei, pe plan orizontal, de la punctul S '. din centru, trageți un cerc și adăugați un triunghi echilateral (Figura 3). Vârfurile lui sunt conectate prin linii drepte cu punctul S '. Cifra rezultată este o proiecție orizontală a piramidei: Δ A'B'C '-
proiecția orizontală a bazei piramidei; S 'este proiecția orizontală a vârfului
și liniile drepte S'A ', S'B'and S'C'-proiecțiile orizontale ale marginilor piramidei. Deoarece baza piramidei este perpendiculară pe planul frontal, proiecția frontală a bazei este dreaptă. Finalizăm proiecția frontală. Prin punctul S 'tragem o linie verticală de comunicare și amânăm de la proiecția frontală a bazei A'B'C' înălțimea piramidei-
dy. Obținem punctul S '' - proiecția frontală a vârfului piramidei. Îl conectăm cu un punct-
Avem proiecția frontală a piramidei, unde S''B''A '' și S''A''C '' -
proiecțiile frontale ale fețelor laterale SBA și SAC. și S''B''C '' - proiecția frontală a posteriorului
marginea SBC. Construim proiecția profilului folosind proiecțiile frontale și orizontale.
Rețineți că planurile fețelor SAB și SAC sunt în poziție generală, iar planul
Pe fața SAB, este dată o proiecție orizontală a punctului K. Este necesar să se construiască un front-
și proiecția profilului acestui punct. Pentru a face acest lucru, trebuie să construim proiecțiile liniei,
aparținând planului poziției generale SAB și trecând prin punctul K. Prin
Proiecția rhizonală K'draws o linie dreaptă 1'2 'paralelă cu partea de bază AB. Po-
TL Beloborodova, E.Yu. Kichigina. Proiecții de polyhedra.