Formule de ecuații pentru rădăcinile ecuațiilor patrate
Fie ecuația cuadratoare ax 2 + bx + c = 0 să fie dat.
Aplicabil axa pătratică trei pe termen-2 + bx + c sunt aceleași transformări pe care le realizăm în § 13 care au demonstrat teorema că graficul funcției y = ax 2 + bx + c este o parabolă.
Avem
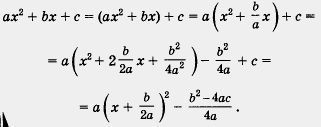
De obicei, expresia b 2 - 4ac și notate cu litera D se numește discriminantul ecuației pătratice ax 2 + bx + c = 0 (sau discriminantul ax pătratice polinom + bx + c).
Prin urmare, ecuația patratică ax2 + u2 + c = 0 poate fi rescrisă în formă
Orice ecuație patratică poate fi transformată în forma (1), care este convenabilă, după cum vom vedea, pentru a determina numărul de rădăcini ale ecuației patrate și a găsi aceste rădăcini.
Dovada. Dacă D <0, то правая часть уравнения (1) — отрицательное число; в то же время левая часть уравнения (1) при любых значениях х принимает неотрицательные значения. Значит, нет ни одного значения х, которое удовлетворяло бы уравнению (1), а потому уравнение (1) не имеет корней.
Exemplul 1. Rezolvați ecuația 2x 2 + 4x + 7 = 0.
Soluția. Aici a = 2, b = 4, c = 7,
D = b 2 -4ac = 4 2. 4. 2. 7 = 16-56 = -40.
Din moment ce D <0, то по теореме 1 данное квадратное уравнение не имеет корней.
Dovada. Dacă D = 0, atunci ecuația (1) ia forma
Este singura rădăcină a ecuației.
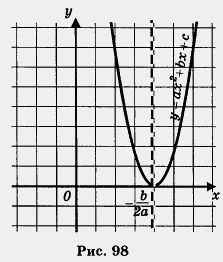
Observație 1. Vă amintiți că x = - este abscisa vârfului parabolului, care servește ca grafic al funcției y = ax 2 + u + c? De ce este asta?
Valoarea a fost singura rădăcină a ecuației patrate ax2 + u2 + c = 0? "Larchik" este deschis pur și simplu: dacă D este 0, atunci, după cum am stabilit mai devreme,
Graficul grafic al funcției este o parabolă cu un vârf la un punct (vezi, de exemplu, Figura 98). Prin urmare, abscisa vârfului parabolului și rădăcina unică a ecuației patrate pentru D = 0 sunt același număr.
Exemplul 2. Rezolvați ecuația 4x 2 - 20x + 25 = 0.
Soluția. Aici a = 4, b = -20, c = 25, D = b 2 - 4 ac = (-20) 2 - 4 • 4 • 25 = 400 - 400 = 0.
Deoarece D = 0, prin Teorema 2 această ecuație quadratică are o rădăcină. Această rădăcină se găsește după formula
Notă 2. Rețineți că 4x2 - 20x +25 este pătratul total: 4x2 - 20x + 25 = (2x - 5) 2.
Dacă am observat acest lucru imediat, am rezolvat ecuația de genul: (2x - 5) 2 = 0, deci 2x = 5 = 0, de unde obținem x = 2.5. În general, dacă D = 0, atunci
ah 2 + bx + c = - aceasta am remarcat mai devreme în Remarca 1.
Dacă D> 0, atunci ecuația cuadratoare ax 2 + bx + c = 0 are două rădăcini care se găsesc prin formule
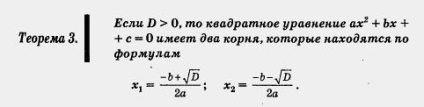
Dovada. Rescriem ecuația patrată ax2 + bx + c = 0 în forma (1)
Am stabilit
Prin ipoteză, D> 0, atunci partea dreaptă a ecuației este un număr pozitiv. Apoi, din ecuația (2), obținem acest lucru

Deci, ecuația patratică dată are două rădăcini:
REMARK 3. În matematică, este foarte rar că termenul introdus nu are, din punct de vedere figurat, fundalul zilnic. Să luăm un nou
noțiunea este o discriminare. Amintiți-vă cuvântul "discriminare". Ce înseamnă asta? Aceasta înseamnă umilirea unora și exaltarea altora, adică atitudine diferită
la oameni diferiți. Ambele cuvinte (atât discriminatorii cât și discriminatorii) derivă din discriminatorii latini - "discriminatorii". Discriminantul distinge între ecuațiile patratice în numărul rădăcinilor.
Exemplul 3. Rezolvați ecuația 3x2 + 8x-11 = 0.
Soluția. Aici a = 3, b = 8, c = -11,
D = b 2 - 4 ac = 8 2 - 4 • 3 • (-11) = 64 + 132 = 196.
Deoarece D> 0, prin Teorema 3 această ecuație patratică are două rădăcini. Aceste rădăcini se găsesc prin formulele (3)
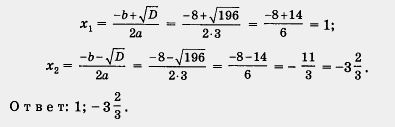
De fapt, am elaborat următoarea regulă:
Regula pentru rezolvarea ecuației
axa 2 + bx + c = 0

Această regulă este universală, se aplică atât ecuațiilor quadrate complete cât și incomplete. Cu toate acestea, ecuațiile patrate incomplete nu rezolvă de obicei această regulă, este mai convenabil să le rezolvăm așa cum am făcut în secțiunea anterioară.
Exemplul 4. Rezolvarea ecuațiilor:
a) x 2 + 3x - 5 = 0; b) - 9x2 + 6x - 1 = 0; c) 2x2-x + 3,5 = 0.
Remarca A) Aici a = 1, b = 3, c = - 5,
D = b 2 - 4ac = 3 2 - 4 • 1 • (-5) = 9 + 20 = 29.
Deoarece D> 0, ecuația cuadratoare dată are două rădăcini. Gasim aceste radacini prin formulele (3)
b) Experiența arată că este mai convenabil să se trateze ecuațiile patratice pentru care coeficientul de conducere este pozitiv. Prin urmare, în primul rând se multiplică ambele părți ale ecuației cu -1, obținem
9x 2 - 6x + 1 = 0.
Aici a = 9, b = -6, c = 1, D = b2 - 4ac = 36 - 36 = 0.
Deoarece D = 0, ecuația quadratică dată are o rădăcină. Această rădăcină se găsește după formula x = -. prin urmare,
Această ecuație ar putea fi rezolvată într-un alt mod: deoarece
9x 2 - 6x + 1 = (3x - IJ, atunci obținem ecuația (3x - I) 2 = 0, de unde găsim 3x - 1 = 0, adică x =.
c) Aici a = 2, b = - 1, c = 3,5, D = b 2 - 4ac = 1 - 4 • 2 • 3,5 = 1 - 28 = -27. <0, то данное квадратное уравнение не имеет корней.
Matematicienii sunt oameni practici, economici. De ce, spun ei, folosiți o regulă atât de lungă pentru rezolvarea ecuației patrate, este mai bine să scrieți imediat formula generală:
Dacă se dovedește că discriminantul D = b 2 - 4ac este un număr negativ, atunci formula scrisă nu are sens (există un număr negativ sub semnul rădăcină pătrată), deci nu există rădăcini. Dacă se dovedește că discriminantul este zero, atunci ajungem
adică, o rădăcină (ei spun, de asemenea, că ecuația patratică are în acest caz două rădăcini identice:
În cele din urmă, dacă se dovedește că b 2 - 4ac> 0, atunci se obțin două rădăcini x1 și x2. care sunt calculate prin aceleași formule (3), după cum se indică mai sus.
Numărul mare în acest caz este pozitiv (ca orice rădăcină pătrată a unui număr pozitiv), și un semn dublu în fața înseamnă că într-un caz (în găsirea x1) este un număr pozitiv, se adaugă la numărul - b, iar în celălalt caz (găsirea x2) acest număr pozitiv este
citiți de la numărul - b.
Aveți libertatea de alegere. Doriți - rezolvați în detaliu ecuația patratică, folosind regula formulată mai sus; doriți - scrieți imediat formula (4) și folosiți-o pentru a trage concluziile necesare.
Exemplul 5. Rezolvarea ecuațiilor:
Soluție, a) Desigur, puteți folosi formulele (4) sau (3), având în vedere că în acest caz Dar de ce să efectuați acțiuni cu fracțiuni, atunci când este mai simplu și, cel mai important, este mai plăcut să tratăți întregi? Să scăpăm de numitorii. Pentru aceasta, trebuie să înmulțim ambele părți ale ecuației cu 12, adică cel mai mic numitor comun al fracțiunilor care servesc ca coeficienți ai ecuației. Avem
din care 8x 2 + 10x - 7 = 0.
Și acum folosim formula (4)
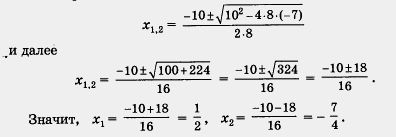
b) Din nou, avem o ecuație cu coeficienți fracționali: a = 3, b = - 0,2, c = 2,77. Se multiplică ambele părți ale ecuației cu 100, apoi obținem o ecuație cu coeficienți întregi:
300x 2 - 20x + 277 = 0.
Mai mult, folosim formula (4):
O estimare simplă arată că discriminantul (radicandul) este un număr negativ. Prin urmare, ecuația nu are rădăcini.
Exemplul 6. Rezolvați ecuația
Soluția. Aici, spre deosebire de exemplul anterior, este preferabil să acționăm conform regulii, și nu prin formula abreviată (4).
Avem a = 5, b = -. c = 1, D = b 2 - 4ac = (-) mai două-4 • • 1 = 60 - = 20 40. Deoarece D> 0, atunci ecuația pătratică are două rădăcini care vor căuta formulele (3)
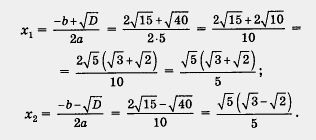
Exemplul 7. Rezolvați ecuația
x 2 - (2p + 1) x + (p 2 + p-2) = 0
Soluția. Această ecuație patratică diferă de toate ecuațiile patrate considerate până în prezent prin faptul că coeficienții nu sunt numere specifice, ci expresii de litere. Aceste ecuații se numesc ecuații cu coeficienți de litera sau ecuații cu parametri. În acest caz, parametrul (litera) p este inclus în compoziția celui de-al doilea coeficient și termenul liber al ecuației.
Să găsim discriminatorii:
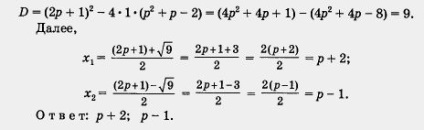
Exemplul 8. Rezolvați ecuația px 2 + (1 - p) x - 1 = 0.
Soluția. Aceasta este, de asemenea, o ecuație cu parametrul p, dar, spre deosebire de exemplul anterior, nu poate fi rezolvată imediat prin formulele (4) sau (3). Faptul este că formulele de mai sus sunt aplicabile ecuațiilor patratice, dar nu putem spune despre ecuația dată. De fapt, ce dacă p = 0? atunci
ecuația ia forma 0 • x 2 + (1-0) x-1 = 0, adică x - 1 = 0, de unde obținem x = 1. Acum, dacă se știe că. atunci putem aplica formulele rădăcinilor ecuației patrate: