Un vector vector de vectori u este un vector nou. înzestrate cu următoarele proprietăți:
1) lungimea sa; și, prin urmare, numeric egal cu aria paralelogramului construit pe aceste vectori ca pe laturi;
2) vectorul este perpendicular pe u;
3) vectori; și formează așa-numita rotație a primului "contrafactor" în sens invers acelor de ceasornic pentru a coincide cu cel de-al doilea vector al factorului, vedem "de la capătul" vectorului ca fiind cel mai scurt, adică (vezi figura) mai mic de 180 °.
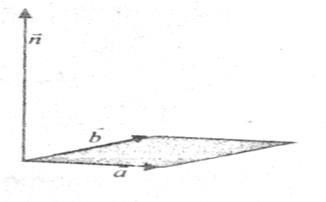
Produsul vector este marcat prin simbolurile sau
și are următoarele proprietăți:
Din aceste proprietăți urmează
Regula pentru calculul unui produs vectorial
Pentru vectorii dat în baza carteziană
produsul lor vectorial poate fi găsit prin formula
Din definiție și proprietăți urmează și
Aplicații de bază ale unui produs vectorial
Dacă S # 8710; este aria triunghiului construit pe vectori și. și # 966; - unghiul dintre ele este
Dacă h este înălțimea piramidei (paralelipiped (prisma)) construită (vezi figura următoare) pe vectori ca pe margini, atunci ea poate fi găsită din
Produs mixt de vectori.
Un produs mixt de trei vectori este un număr egal cu produsul scalar al produsului vectorial al primilor doi vectori de către al treilea.
Denumirea produsului mixt de simbolul (), prin definiție, avem
În baza carteziană, produsul mixt al vectorilor
se calculează prin formula
Din punct de vedere geometric, modulul produsului mixt () este egal cu volumul paralelipipedului, construit pe vectori ca pe margini. Din aceasta, în special, rezultă că este egal cu volumul dublu al prismei corespunzătoare și cu volumul "descendent" al piramidei cu aceleași coaste.