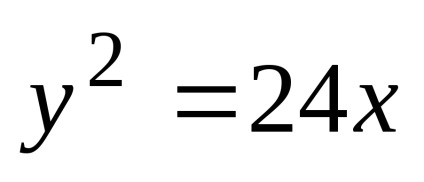O elipsă este locul punctelor dintr-un plan, pentru fiecare dintre acestea suma distanțelor față de două puncte date ale acestui plan, numită focare, este constantă și mai mare decât distanța dintre focare.
Semnificăm prin

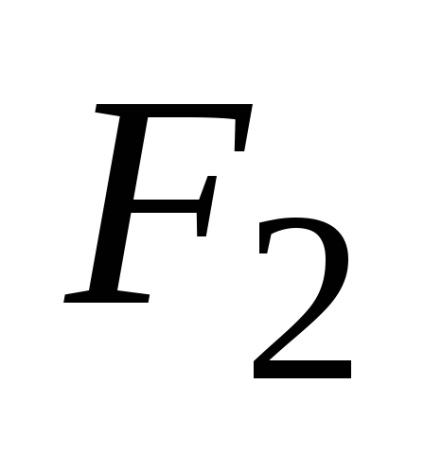
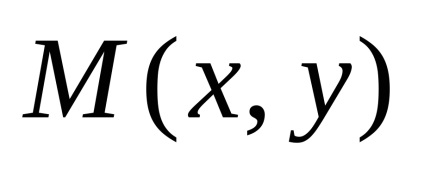
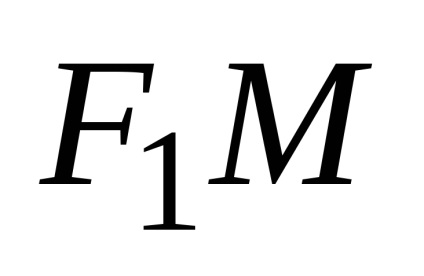
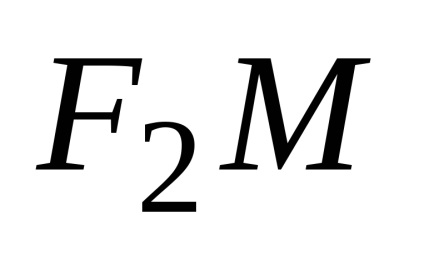
Noi denotăm,
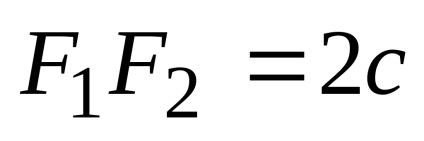
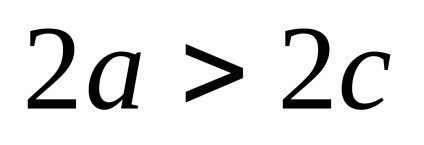

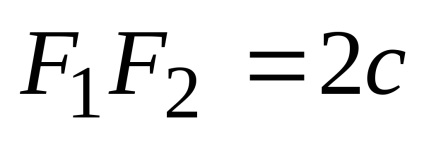
Această ecuație este ecuația elipsei. După transformările sale, putem obține o ecuație mai simplă
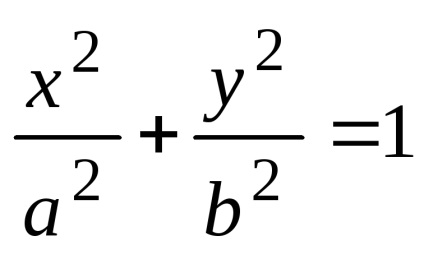
care se numește ecuația canonică a unei elipse. În această ecuație
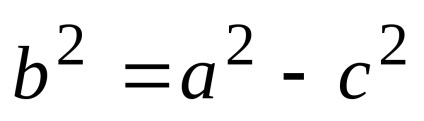
Dacă focalizarea elipsei se află pe axa Ox. apoi a> b. În acest caz, a se numește axa semi-majoră a elipsei, iar b este semiaxisul mic. atitudine
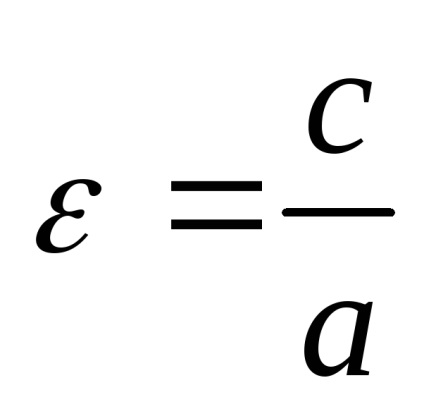
Dacă în ecuația elipsei b = a. atunci se transformă în ecuație
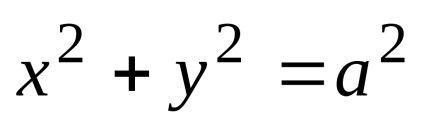
Exemplul 1. Scrieți ecuația elipsei a cărei axă majoră coincide cu axa Ox și este egală cu 10, iar distanța dintre focuri este 8.
Soluția. Prin ipoteză
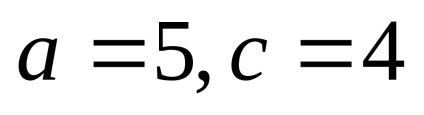
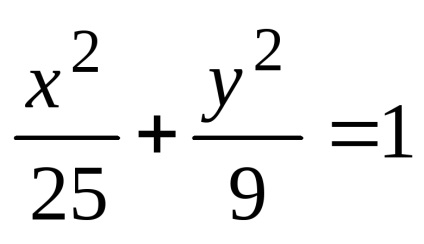
Hyperbola este locusul punctelor unui plan, pentru fiecare dintre acestea valoarea absolută a diferenței de distanță față de două puncte date ale acestui plan, numită focare, este constantă și mai mică decât distanța dintre focare.
Semnificăm prin

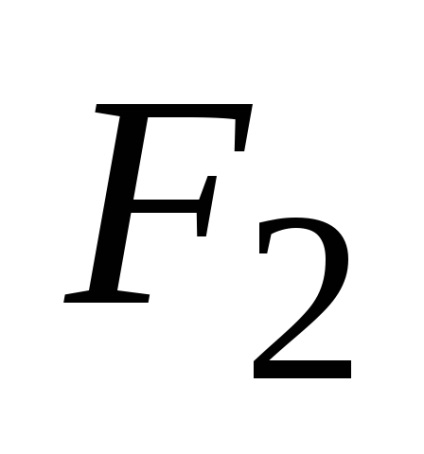
Distanța dintre focuri este marcată cu
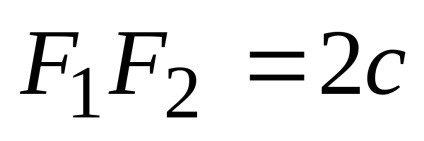
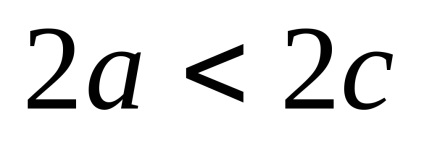

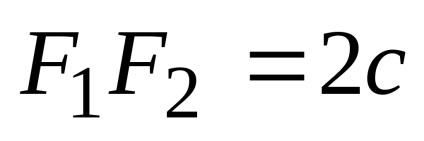
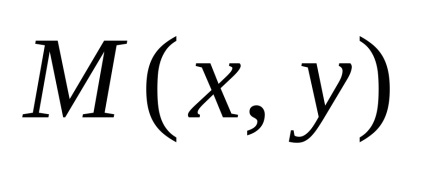

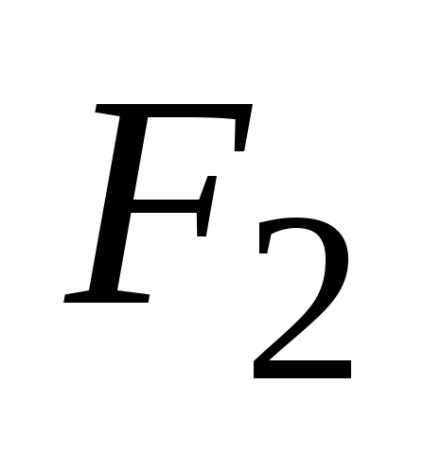
Ecuația obținută este ecuația hiperbola. După transformările sale, putem obține o ecuație mai simplă
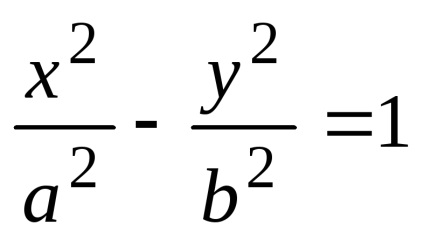
care se numește ecuația canonică a hiperboliei. În această ecuație
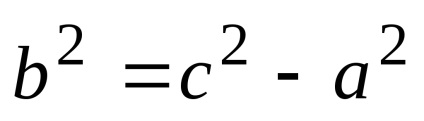
Numărul a se numește semiaxis real al hiperboliei, iar numărul b se numește semiaxis imaginar. ecuație
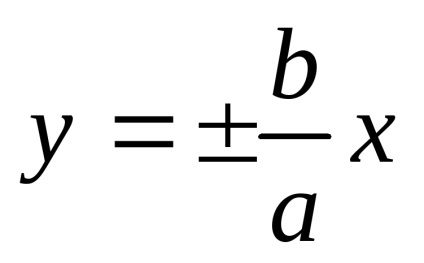
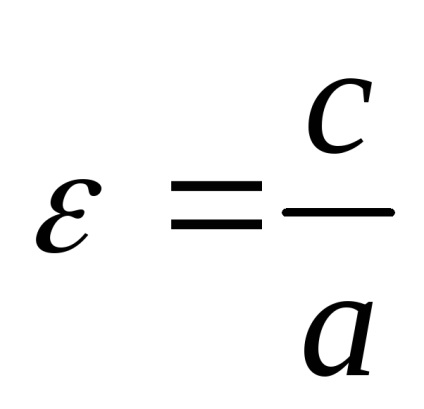
Exemplul 2. Axa reală a hiperboliei
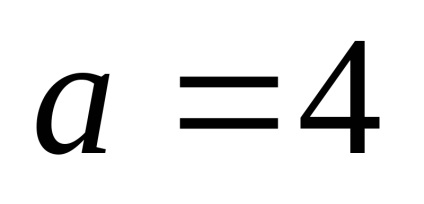
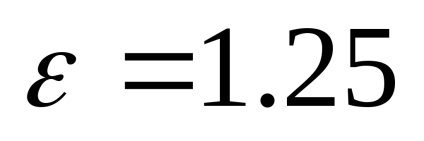
Soluția. Deoarece excentricitatea hiperboliei
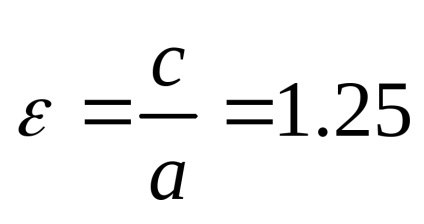
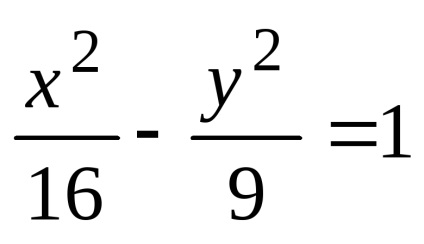
O parabolă este locusul punctelor pe plan, pentru fiecare dintre acestea distanța până la un punct fix al planului numită focalizare este egală cu distanța față de o anumită linie fixă numită directrix.
Fie F focalizarea și p distanța de la focalizare la directrix. Cantitatea p este numită parametrul parabola. Pe parabolă luăm un punct arbitrar
Având în vedere notațiile acceptate, se poate scrie
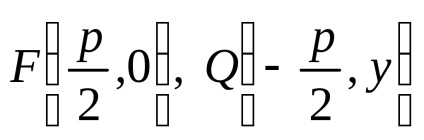
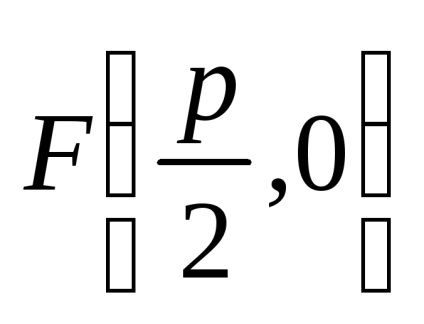
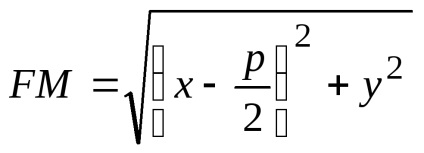
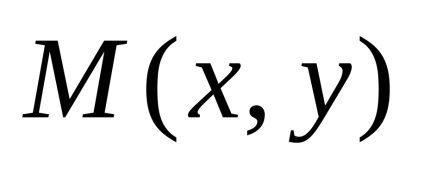
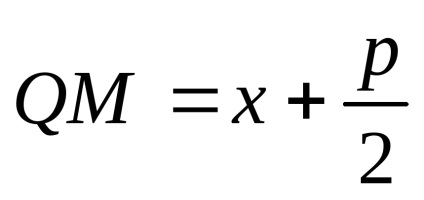
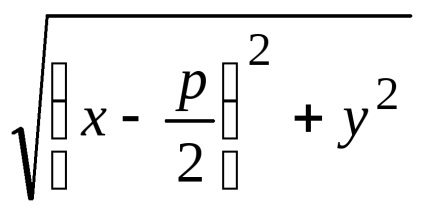
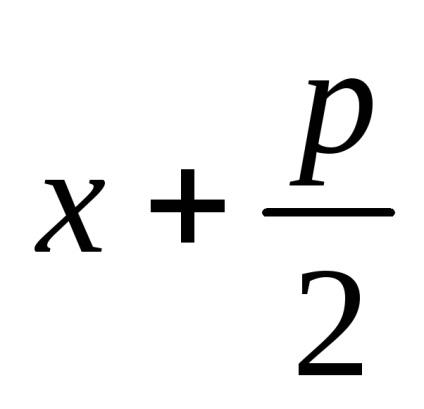
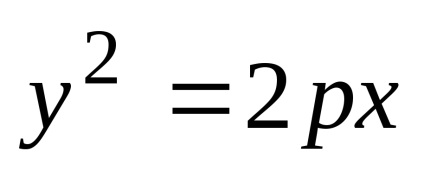
care se numește ecuația canonic parabola.
Întrebări pentru auto-monitorizare a cunoștințelor
Ce se numește o elipsă și cum se scrie ecuația canonică?
Ce se numește excentricitatea elipsei și ce caracterizează aceasta?
Ce se numește hiperbolă și cum este scrisă ecuația canonică?
Care sunt asimptotele unei hiperbola?
Ce se numește o parabolă și cum se scrie ecuația canonică?
Sarcini pentru munca independentă
Determinați semiaxele și coordonatele focarelor de elipse
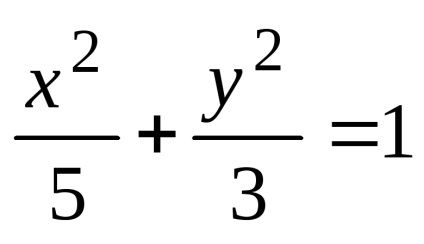
Scrieți ecuația canonică a elipsei a cărei axă semimajor este 5, iar excentricitatea este de 0,6.
Scrieți ecuația canonică a hiperboliei dacă focurile ei se află pe axă
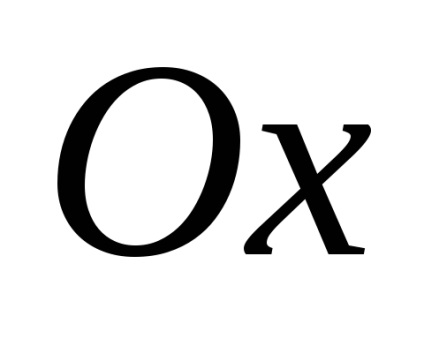
Găsiți lungimile axelor, coordonatele focarelor, excentricitatea și ecuațiile pentru asimptotele hiperboliei.
Găsiți ecuația directrix și focalizarea parabolei