Cu metoda introducerii unei noi variabile în rezolvarea ecuațiilor raționale cu o variabilă, ați fost introduși în cursul algebrei clasei a VIII-a. Esența acestei metode în rezolvarea sistemelor de ecuații este aceeași, dar din punct de vedere tehnic există anumite trăsături pe care le vom discuta în exemplele de mai jos.
Exemplul 3. Rezolvați sistemul de ecuații
Soluția. Introducem o nouă variabilă. Apoi prima ecuație a sistemului poate fi rescrisă într-o formă mai simplă: Rezolvăm această ecuație în raport cu variabila t:

Ambele valori satisfac condițiile. și deci sunt rădăcini ale unei ecuații raționale cu variabila t. Dar inseamna, fie din locul unde gasim ca x = 2y, fie
Astfel, cu ajutorul metodei de introducere a unei noi variabile am reușit să "stratificăm" prima ecuație a sistemului, care este destul de complexă în formă, în două ecuații mai simple:
Ce urmează? Și apoi fiecare dintre cele două ecuații simple obținute ar trebui să fie luată în considerare alternativ într-un sistem cu ecuația x 2 - y 2 = 3, pe care încă nu am reamintit-o. Cu alte cuvinte, problema reduce la rezolvarea a două sisteme de ecuații:
Este necesar să se găsească soluțiile primului sistem, cel de-al doilea sistem și toate perechile de valori rezultate pentru a fi incluse în răspuns. Rezolvăm primul sistem de ecuații:
Folosim metoda substituției, mai ales că totul este gata pentru el aici: înlocuim expresia 2y pentru x în a doua ecuație a sistemului. Avem
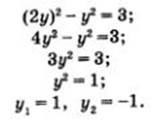
Deoarece x = 2y, găsim, respectiv, x1 = 2, x2 = 2. Astfel, se obțin două soluții ale sistemului dat: (2; 1) și (-2; Rezolvăm al doilea sistem de ecuații:
Din nou, folosim metoda substituției: înlocuim expresia 2x pentru y în a doua ecuație a sistemului. Avem
Această ecuație nu are rădăcini, deci sistemul de ecuații nu are soluții. Astfel, în răspunsul este necesar să se includă numai soluțiile primului sistem.
Metoda de introducere a variabilelor noi în sistemele de rezolvare a două ecuații cu două variabile este utilizată în două versiuni. Prima opțiune este să introduceți o nouă variabilă și să o utilizați numai într-o singură ecuație a sistemului. Acesta este exact cazul din Exemplul 3. A doua opțiune: două variabile noi sunt introduse și utilizate simultan în ambele ecuații ale sistemului. Acesta va fi cazul în exemplul 4.
Exemplu 4. Rezolvați sistemul de ecuații