Traseul aeronavei între două date de pe hartă poate fi depus de-a lungul ortodromului sau loxodromului. Alegerea modului de rulare depinde de echipamentul aeronavei cu echipament de navigație. Fiecare dintre aceste linii de cale are anumite proprietăți.
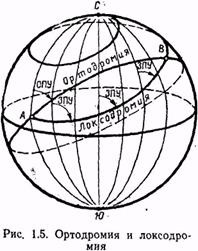
Ortodromia este un arc de cerc mare, care este cea mai scurtă distanță dintre două puncte A și B de pe suprafața globului (Figura 1.5).
Ortodromul are următoarele proprietăți:
1) este linia celei mai scurte distanțe dintre două puncte de pe suprafața globului;
2) traversează meridianele sub unghiuri diferite, inegale datorate convergenței meridianelor la poli.
Ecuatorul și meridianele sunt cazuri speciale de ortodromie. Prin două puncte de pe suprafața pământului nu este dispus la capetele opuse ale liniei drepte care trece prin centrul Terr-li, poate deține un singur cerc mare. Cale De acord Mallett sa-numita mare cerc ortodromică, și direcția de zbor Leniye orthodromy indică unghiul marginea drumului ortodromică (GTC) între direcția nord și calea predeterminată meridianul linie leniem la punctul de pornire orthodromy. În cazul particular în care orthodromy coincide cu Me-ridianom sau ecuator unghiul de cale ortodromică rămâne constantă și egală cu primul caz 0 sau 180 °, iar în al doilea - 90 ° sau 270 °.
Zborul de mare cerc de un fir de busolă magnetică vypol nu poate, pentru că, în acest caz, ar fi necesar să se schimbe direcția de zbor a aeronavei de la meridianul de meridianul care viespe există practic imposibil. Prin urmare, un astfel de zbor este realizat cu ajutorul unor instrumente speciale de curs de schimb - giroscopul sau sistemul de cursuri.
Pe harta de zbor, redactat într-un Polikon-cal de proiecție orthodromy modificată între două puncte este-TION la o distanță de 1000-1200 km, prevăzută o linie dreaptă, și la distanțe mai mari - linia curbată, care este convexă la polul. În primul caz, SDA și lungimea căii de-a lungul ortodromului sunt măsurate pe hartă. În al doilea caz, orthodromy fiind mapate la punctele intermediare, iar lungimea unui cerc mare EPP-ti ny calculat conform formulelor speciale.
Ca date inițiale pentru calculul matematic al SDA și lungimea ortodromului, coordonatele geografice ale punctelor sale inițiale și finale servesc. Aceste coordonate sunt determinate cu o precizie de până la un minut în directoarele relevante sau luate direct pe hartă de zbor.
Lungimea căii de-a lungul ortodromiei între două puncte este calculată de formula
cos Sortare = sinφ1 sinφ2 + cosφ1 cosφ2cos (λ2 - λ1),
unde Sorth este lungimea căii de-a lungul ortodromiei în grade de arc; φ1 și λ1 sunt coordonatele punctului de plecare al ortodromiei; φ2 și λ2 sunt coordonatele punctului final al ortodromiei.
Pentru a obține lungimea căii de ortodromie în kilometri, trebuie să obțineți rezultatul din formula pentru a exprima în câteva minute arc și să se înmulțească cu 1.852 km.
Unghiul ortodromic al liniei (direcția ortodromului la punctul de origine al traseului) se calculează prin formula
ctgα = cosφ1 tgφ2 cosec (λ2 - λ1) - sinφ, ctg (λ2 - λ1).
Pentru o lungă perioadă de timp, ortodromia este reprezentată pe hartă la punctele intermediare. Coordonatele φ și λ ale acestor puncte sunt calculate prin formula
tgφ1 = Asin (λ - λ1) + Bsin (λ2 - λ), tgφ2
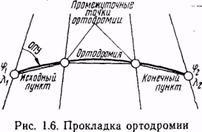
În acest caz, este de obicei dată de lungimea λ (prin 10-20 °) și se determină latitudinea φ a fiecărui punct intermediar. Coeficienții A și B pentru toate punctele intermediare rămân neschimbate. Pentru a asigura o precizie ridicată a rezultatelor finale, calculul conform formulelor indicate este efectuat în conformitate cu tabelele cu cinci valori ale funcțiilor trigonometrice. Prin calcularea coordonatelor punctului aplicate PROM-diate pe hartă, și apoi transportate prin aceste puncte o-core sub forma unei linii curbe netede (fig. 1.6) sau un efect direct-ing segmentul care leagă calea ortodromică intersecŃii.
Calculul matematic al ortodromiei oferă o precizie bună, dar este asociat cu calcule greoaie. De aceea, uneori, ORTOD-zbor romiyu aplicat la masina-navigare folosind un glob sau plasă, făcute în pro-polare proiecțiile centrale, care-clorhidric orthodromy pentru orice distanță este reprezentată printr-o linie dreaptă. Folosind această proprietate a rețelei, puteți efectua un calcul grafic al ortodromului. Pentru a face acest lucru, pe grilă, conectați punctele inițiale și finale ale ortodromului cu o linie dreaptă. Punctele intermediare sunt trase pe această linie. Apoi, prin coordonate, ele sunt transferate pe harta de zbor și prin punctele obținute pe harta de zbor se efectuează orthodromia.
Zborul de la un punct la altul pe o busolă magnetică este convenabil să se realizeze cu un unghi constant al pistei, adică prin loxodromie.
Loxodromia este o linie care traversează meridianele la aceleași unghiuri de călătorie. Calea unui avion pentru loxodromia se numește loxodrom. Unghiul constant la care loxodromia traversează meridianele se numește unghiul de rulare loxodromic.
Pe suprafața liniei de glob rombice este un fel de simplu ranstvennoy spirală logaritmică, care merge în jurul lumii de nenumărate ori și cu fiecare rândul său, treptat, aproximative-zhaetsya la polul, dar niciodată nu ajunge la ea (vezi. Fig. 1.5). Calea de linie rombice este întotdeauna mai mare decât calea cerc mare. Numai în Cha-stnyh, atunci când are loc un zbor pe meridianul sau ecuator-Torul, lungimea căii pe linia rombice și cercul mare va fi la fel.
Dacă punctele de zbor nu sunt foarte îndepărtate una de cealaltă, diferența în calea de-a lungul ortodromiei și loxodromului este nesemnificativă. Diferența este, de asemenea, mică la distanțe mari de zbor, dacă traseul trece printr-un unghi de cel mult 20 ° față de meridian. La distanțe mari între punctele de călătorie și în special atunci când la bord traseu aproape de 90 sau 270 °, diferența dintre rasele, Stoyanov mare cerc și atinge valori mari-loxodrome Cheny. Cu un traseu lung, traseul de-a lungul ortodromului reduce foarte mult distanța, reduce timpul de zbor și consumul de combustibil, ceea ce mărește încărcătura utilă a aeronavei. Prin urmare, zborurile de aeronave de transport supersonice sunt efectuate pe căile respiratorii îndreptate care coincid cu ordonanțele.
Loxodromia are următoarele proprietăți:
1) traversează meridianele la un unghi constant și pe suprafața globului, cu proeminența îndreptată spre ecuator;
2) calea de-a lungul loxodromiei este întotdeauna mai lungă decât calea de-a lungul ortodromului, cu excepția cazurilor particulare în care zborul are loc de-a lungul meridianului sau de-a lungul ecuatorului. Paralele sunt cazuri particulare de lok-sodromiya.
În cazul în care zboară pe distanțe lungi diferența în calea liniei rombice o-Drome și nu pot fi neglijate. Prin urmare, ruta de zbor în continuare, în cazul în care punctele intermediare nu sunt definite pentru daniem-ar trebui să fie pus pe cercul mare. În practică, domeniul-ing pe liniile aeriene aprobate, care sunt stabilite anumite reguli HN, traseul nu este o linie dreaptă de la punctul de plecare până la punctul de debarcare, și are niște îndoituri. segmente de linie dreaptă este selectată astfel încât diferența în unghiuri de deplasare la începutul și porțiunea de capăt nu depășește 2 °. Cu această alegere a lungimii secțiunilor de LZP este pus pe harta de zbor sub forma unei linii drepte, care a fost luată ca rombice linie, în cazul în care direcția de zbor este menținută de busola magnetică, sau cercul mare, în cazul în care direcția de zbor este menținută de un instrumente de schimb valutar-spe cial. În acest caz, calea de loxodromic se va abate ușor de la o linie dreaptă, și pentru segmentele de 200-250 km aproape coincide cu traseul dorit, a pus pe o hartă.