O astfel de piață uimitoare și familiară. Este simetric cu privire la centrul și axele sale trase de-a lungul diagonalelor și prin centrele laturilor. Iar pentru a căuta suprafața unui pătrat sau a volumului său nu reprezintă o mare dificultate. Mai ales dacă este cunoscută lungimea lui.
Câteva cuvinte despre cifră și proprietățile sale
Primele două proprietăți sunt legate de definiție. Toate laturile figurii sunt egale una cu alta. Până la urmă, pătratul este drept patrulater. Și el în mod necesar toate părțile sunt egale și unghiurile au aceeași valoare, și anume - 90 de grade. Aceasta este a doua proprietate.
Al treilea este legat de lungimea diagonalelor. Ele sunt, de asemenea, egale unele cu altele. Și se intersectează în unghiuri drepte și în punctele de mijloc.
O formulă în care se folosește numai lungimea laturii
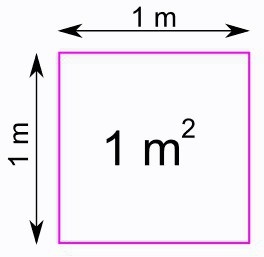
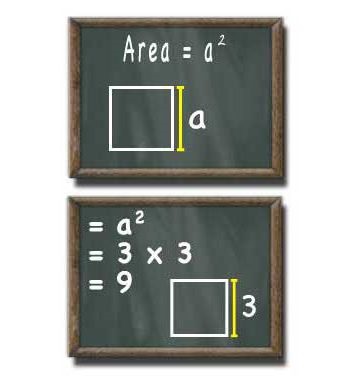
În primul rând despre desemnare. Pentru lungimea laturii, este obișnuit să alegeți litera "a". Apoi pătratul pătratului se calculează după formula: S = a 2.
Este ușor de obținut din cel cunoscut pentru dreptunghi. În ea, lungimea și lățimea sunt înmulțite. Pentru un pătrat, aceste două elemente sunt egale. Prin urmare, pătratul acestei cantități apare în formula.
Formula în care apare lungimea diagonalei
Este ipoteza din triunghi, ale cărei picioare sunt laturile figurii. Prin urmare, putem folosi formula teoremei pitagoreene și putem deduce o egalitate în care partea este exprimată prin diagonală.
Realizând astfel de transformări simple, obținem că pătratul pătratului prin diagonală se calculează după următoarea formulă:
S = d 2 / 2. Aici litera d indică diagonala pătratului.
Formula în jurul perimetrului
Într-o astfel de situație este necesar să se exprime partea laterală prin perimetru și să se substituie formulei din zonă. Deoarece există patru laturi ale figurii, perimetrul va trebui împărțit la 4. Aceasta va fi valoarea laturii, care poate fi apoi înlocuită cu cea inițială și cu suprafața pătratului.
Formula în formă generală este după cum urmează: S = (P / 4) 2.
Acțiuni de decontare
Nu. 1. Există un pătrat. Suma celor două laturi este de 12 cm. Calculați suprafața pătratului și perimetrul acestuia.
Soluția. Deoarece suma celor două părți este dată, trebuie să cunoașteți lungimea uneia. Deoarece acestea sunt identice, numărul cunoscut trebuie împărțit în două. Adică partea din această cifră este de 6 cm.
Apoi perimetrul și suprafața sa pot fi ușor calculate din formulele de mai sus. Primul este de 24 cm, iar al doilea este de 36 cm2.
Răspuns. Perimetrul pătratului este de 24 cm, iar suprafața sa este de 36 cm2.
2. Aflați zona pătratului cu un perimetru de 32 mm.
Soluția. Este suficient să înlocuiți valoarea perimetrului cu formula de mai sus. Deși puteți cunoaște mai întâi partea pătratului și apoi zona acestuia.
În ambele cazuri, acțiunile vor merge mai întâi la divizare și apoi la exponentiere. Calculele simple conduc la faptul că suprafața pătratului prezentat este de 64 mm2.
Răspuns. Suprafața solicitată este de 64 mm2.
Partea pătratului este de 4 dm. Dimensiunile dreptunghiului: 2 și 6 dm. Care dintre cele două figuri are mai multă arie? Cât de mult?
Soluția. Lăsați partea de pătrat să fie notată cu litera a1. apoi lungimea și lățimea dreptunghiului a2 și b2. Pentru a determina pătratul pătratului, valoarea lui a1 se presupune a fi pătrat, iar dreptunghiul pentru a multiplica a2 și b2. E ușor.
Se pare că pătratul pătratului este de 16 dm 2. iar dreptunghiul este de 12 dm 2. Este evident că prima cifră este mai mare decât a doua. Aceasta este în ciuda faptului că acestea sunt egale, adică au același perimetru. Pentru a verifica, puteți număra perimetrele. La pătrat, partea trebuie să fie înmulțită cu 4, se dovedește a fi 16 dm. La dreptunghi, pliați laturile și multiplicați cu 2. Va fi același număr.
În sarcină este încă necesar să răspundem, câte domenii diferă. Pentru aceasta, un număr mai mic este scăzut de la un număr mai mare. Diferența este de 4 dm 2.
Răspuns. Pătraturile sunt 16 dm 2 și 12 dm 2. Pătratul este mai mare cu 4 dm 2.
Problema dovezii
Stare. Un dreptunghi este construit pe izotopul unui triunghi drept al isoscelului. La înălțimea sa de hipotensiune este construită pe care este construit un alt pătrat. Dovedeste ca zona primei este de doua ori mai mare decat a doua.
Soluția. Introducem notația. Fie catela să fie egală cu a, iar înălțimea pentru hipotensiune, x. Zona primului pătrat este S1. al doilea - S2.
Pătratul pieței construit pe picior este ușor de calculat. Se dovedește a fi egală cu a 2. Cu a doua valoare, totul nu este atât de simplu.
Mai întâi trebuie să știți lungimea hypotenusei. Pentru aceasta, formula teoremei pitagoreene este utilă. Transformările simple duc la următoarea expresie: a√2.
Deoarece înălțimea într-un triunghi izoscel atrăgat de bază este de asemenea mediană și înălțime, ea divide un triunghi mare în două triunghiuri egale, egale, drept. Prin urmare, înălțimea este jumătate din hypotenuse. Asta este, x = (a√2) / 2. Prin urmare, este ușor să aflați zona S2. Se obține ca 2/2.
Evident, valorile înregistrate diferă exact cu un factor de două. Și al doilea este de câteva ori mai mic. După cum este necesar pentru a dovedi.
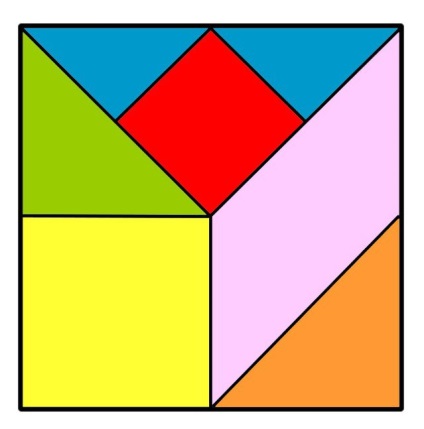
Un puzzle neobișnuit - tangram
Este făcut dintr-un pătrat. Este necesar să o tăiați în diverse forme conform anumitor reguli. Totalul pieselor trebuie să fie de 7.
Regulile presupun că în timpul jocului vor fi utilizate toate detaliile rezultate. Dintre acestea, trebuie să faceți alte forme geometrice. De exemplu, un dreptunghi, un trapez sau o paralelogramă.
Dar este chiar mai interesant atunci când siluetele de animale sau obiecte sunt obținute din bucăți. Și se pare că suprafața tuturor figurilor derivate este egală cu cea a pătratului inițial.
