Prezentare pe tema: "Soluția inegalităților raționale prin metoda intervalului Scop: prin rezolvarea inegalităților prin metoda intervalului, luați în considerare cazuri speciale - rădăcinile chiar și a multiplicității și punctelor". - Transcriere:
1 Soluția inegalităților raționale prin metoda intervalului Obiectiv: rezolvarea inegalităților prin metoda intervalului, luarea în considerare a cazurilor speciale - rădăcini de multiplicitate și punct de discontinuitate. Definiție: În mod rațional, înțelegem inegalitățile care conțin doar numere raționale sau funcții fracțional-raționale.

2 Metoda de intervale este după cum urmează: Linia numerică este împărțită la zero a funcției într-un număr finit de intervale, fiecare dintre ele funcția păstrând semnul.

3 Când se schimbă funcția? Concluzie: când treceți prin zero.
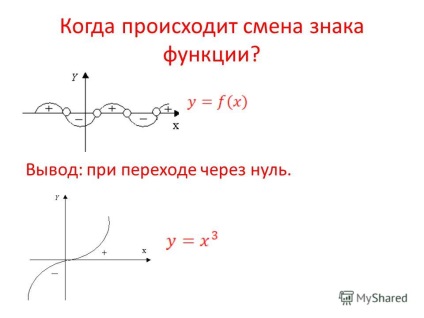
5 Concluzie: o expresie care este numerotată în par, nu afectează semnul inegalității, ci influențează decizia și o elimină fără restricții suplimentare.

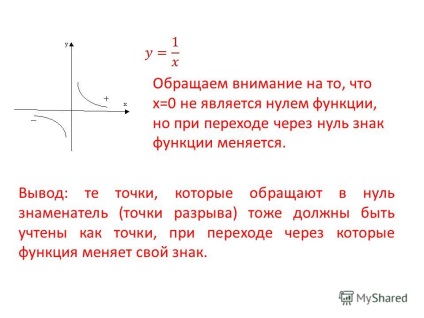
6 Atragem atenția asupra faptului că x = 0 nu este zero a funcției, dar când trece prin zero, semnul funcției se schimbă. Concluzie: acele puncte care anulează numitorul (punctele de discontinuitate) ar trebui de asemenea luate în considerare ca puncte, trecând prin care funcția își schimbă semnul.
7 Considerăm soluția inegalității: Concluzia: x = -2 este o rădăcină chiar și a multiplicității, atunci când trece prin această funcție semnul nu se schimbă.

9

10
11

12
Rezolvarea inegalităților: 77 (c, d) 78 (c, d, e) 80 (a) 81 (c)
