MAI MULTE MATERIALE PE TEMA:
Găsiți valoarea curentă a fluxului de plată definit de
după cum urmează: primul an - încasări 500 am. USD.,
al doilea an - venit 200 am. al treilea an - plata
400 am. încă șapte ani - un venit de 500 de ore. de dolari.
Rata de actualizare este de 6% pe an.
Soluția
În acest exemplu, fluxul de plăți în ultimele șapte
ani este o anuitate permanentă. Prin formula (7.5)
putem calcula valoarea sa moderna Aq. Este imposibil
se va întâmpla ca aceasta să fie valoarea actuală la momentul începerii
a patra perioadă:
A0 = 500 • 5,58 = 2791 (US $)
(coeficienții de reducere sunt prezentați în tabelul 4 din apendice).
Nia 2). Mai mult, folosind formula (3.11), găsim moderne
valoare în momentul în care debitul de plată începe pentru toate cele rămase
plăți și sume A0:
A \ = 500 -0,953 = 471,5 (dolari SUA);
A2 = 200 • 0,89 = 178 (US $);
Аь = -400 • 0,840 = -336 (dolari SUA);
А4 = 2791 • 0,840 = 2344,44 (dolari SUA).
Adăugând valorile rezultate, găsim cele moderne
fața întregului flux de plăți:
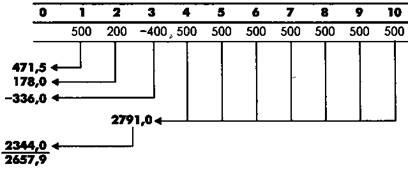
Valoarea curentă a anuității
În toate cazurile, când este într-un flux arbitrar
plăți există loturi care pot fi
sunt descrise ca fiind constante sau schimbate de unii
legea anuităților, ar trebui să se acorde atenție
și termenul acestor anuități, care nu coincid
cu momentul inițial și cu termenul întregului flux de plăți.
Următoarea etapă a studiului nostru este conversia anuităților.
Conform conversiei anuității se înțelege o astfel de modificare în
anuitate, după care o nouă anuitate
ar fi echivalentă cu asta.
Două anuități sunt considerate echivalente dacă co-
valorile de timp reduse la același moment
timp.
În practică, este necesar să se calculeze parametrii echivalentului
Anuitatea apare adesea când condițiile se schimbă.
plata datoriilor, rambursarea unui împrumut sau a unui împrumut etc. În același timp,
Versiunea poate apărea imediat după ce anuitatea începe (pentru aceasta
momentul și valorile moderne ale echivalentului
anuități) și după plata unor anuități
TA. În acest ultim caz, toate calculele sunt efectuate pentru restul datoriei
la momentul transformării.
Luați în considerare cele mai frecvente cazuri de conversie
Anuități anuale.
1. După un anumit interval de timp n0 (poate fi pa-
venele și 0) după începutul anuității, întreaga datorie reziduală poate fi
plătită o singură dată (răscumpărarea de anuitate). Este evident că în acest sens
Dacă suma plătită este egală cu cea curentă
mărimea reziduului de anuitate calculat pentru termenul n1 = n - W0 -
2. Este posibil să apară o problemă care este inversă față de cea precedentă:
rambursarea în rate, sub forma unei plăți anuitate permanente,
și este necesar să se determine unul dintre parametrii anuității pentru
date ale restului. Deoarece valoarea datoriei este cunoscută aici, adică,
valoarea actuală a anuității, pentru a găsi necunoscutul
parametru, folosim formulele (7.8) sau (7.10).
3. Perioada de rambursare a datoriilor poate fi modificată în timp ce se menține
din rata dobânzii anterioare. Valoarea plății P1 pentru perioada W1
găsim, folosind ecuațiile de echivalență (equate-
valorile moderne ale anuităților):
Evident, dacă termenul de anuitate crește, valoarea P co-
și invers.
4. Este posibil să existe o situație în care suma de plată P
trebuie să fie schimbată într-o parte sau alta. Luați în considerare acest lucru
din exemplul 28.