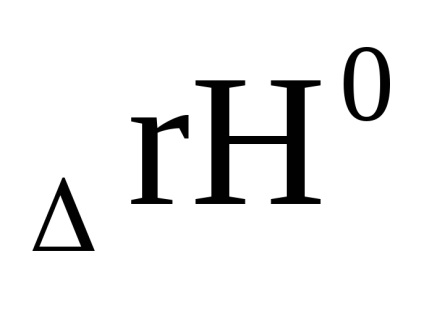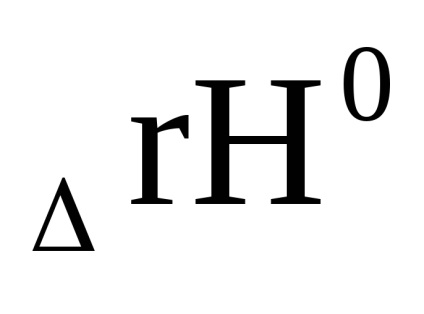0 + RT Inn
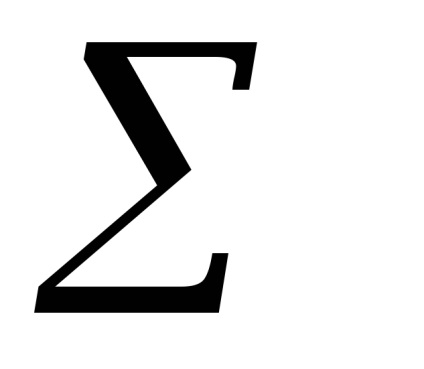

(presiunile parțiale se referă la o stare de neechilibru)
Suma din primul bracket, așa cum se arată în ecuația derivată (1.84) cu condiția Δ G = 0, este -RT lnKp. Prin urmare, Δr G = -RT lnKp + RT (cp'C + dp'D - ap'A - bp'B) sau
Δr G = RT (ln
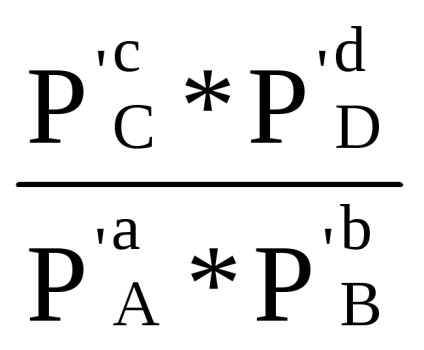
Ecuația rezultată se numește ecuația izotermică a reacției chimice (sau ecuația lui Van't Hoff, 1886), relatează energia Gibbs a reacției la constanta echilibrului chimic și presiunea parțială inițială a substanțelor care reacționează.
Dacă presiunea parțială a tuturor siturilor de reacție din amestecul inițial este egală cu unitatea (pi = 1), atunci rezultă din ecuația (1.87) că
Δr G 0 = -RT ln Kp (1,88)
Cantitatea Δr G 0 este potențialul reacțional izobaric-izotermic standard la temperatura aleasă T. După înlocuirea lui -RTlnKp cu Δr G 0, ecuația (1.87) are următoarea formă:
Δr G = Δr G 0 + RT ln
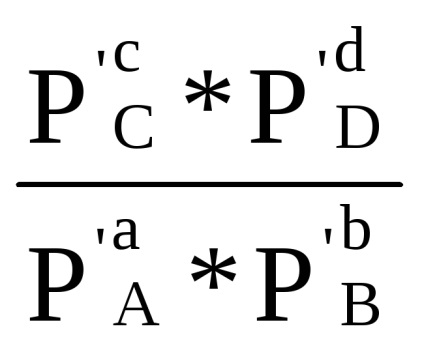
Se poate observa din ecuație că schimbarea potențialului de reacție izobaric-izotermic constă în două părți. O parte Δr G 0 este o schimbare pentru o reacție ipotetică în care toți reactanții sunt luați în stare standard. Pentru această reacție, Δr G0 este o valoare constantă pentru p, T, în funcție de natura participanților la reacție. Al doilea termen din ecuația (1.89) reflectă dependența Δr G 0 asupra compoziției lanțului de reacție.
Aceasta reprezintă o creștere a potențialului izobaric-izotermic, care se obține prin trecerea substanțelor de reacție luate la orice presiune parțială (concentrație) în produse de reacție, luată la orice presiune parțială.
Dependența constantei de echilibru la temperatură. Ecuația izobarului reacției.
Echilibrul chimic este dinamic, se schimbă într-o direcție sau alta pe măsură ce condițiile externe se schimbă. În particular, poziția de echilibru și, în consecință, constanta de temperatură afectează constanta de echilibru.
Dependența funcțională a constantei de echilibru la temperatură la presiune constantă poate fi obținută din ecuația izotermelor de reacție (1.87) și a ecuației Gibbs-Helmholtz (1.70).
Se diferențiază ecuația izotermei reacției (1.87) în funcție de temperatură, ținând seama de faptul că p'A. p'B. r'S. p'D sunt date și nu depind de temperatură, obținem
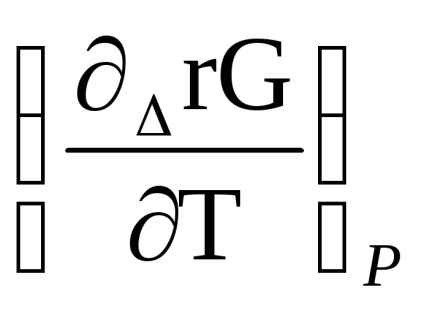
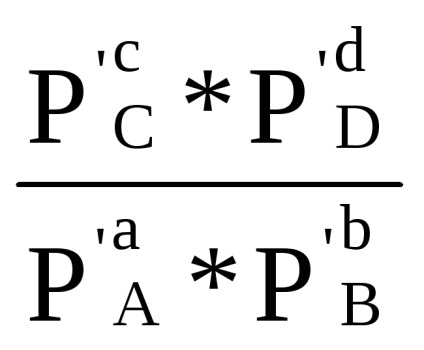
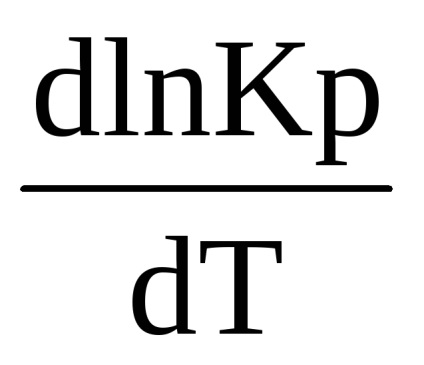
Înlocuim în ecuația lui Gibbs-Helmholtz:
Δr G (m) = Δr H (m) + T [
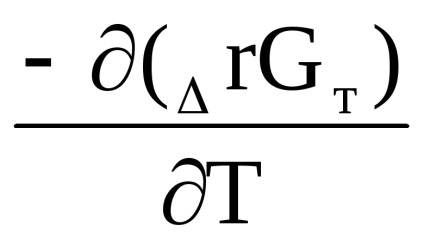
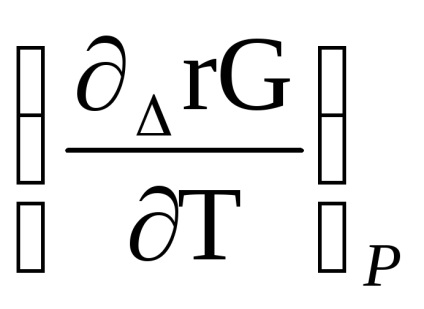
RTln
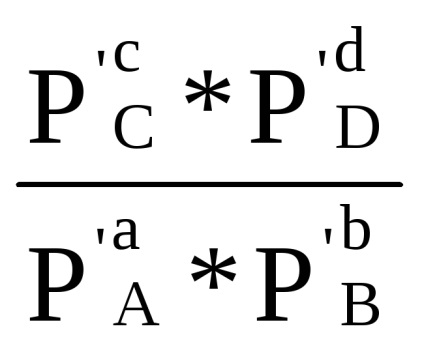
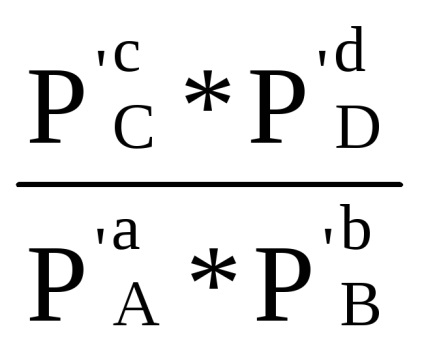
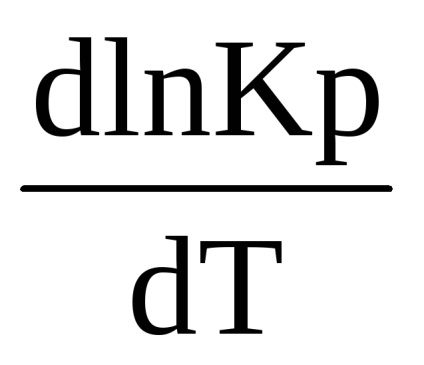
După reducere, obținem:
Această ecuație stabilește relația dintre modificarea constantei de echilibru cu temperatura și efectul termic al reacției. Se referă la procesele care se produc la presiune constantă și se numește ecuația izobar (Vant-Hoff, 1885)
Pentru a calcula echilibrul pentru temperaturi diferite, trebuie integrată ecuația (1.90). După separarea variabilelor, avem
Într-un domeniu de temperatură îngust, efectul termic al reacției este practic independent de temperatură, adică Δp = 0. Prin urmare, după integrare, obținem
unde B este constanta de integrare.
Comparația ecuației (1.91) cu ecuația (1.88a) arată că B =
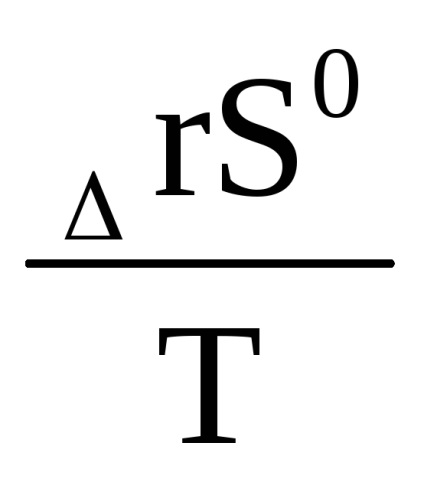
Ecuația (1.91) menționată în condițiile standard poate fi scrisă sub forma:
unde
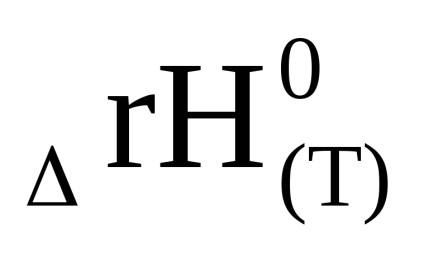
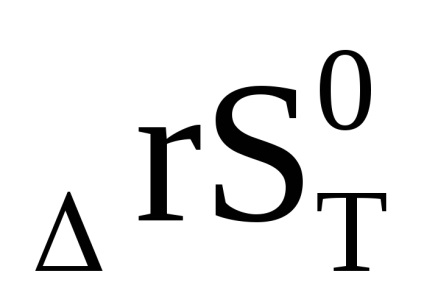
Rezultă din ecuația (1.92) că ln Kp și, în consecință, constanta de echilibru poate, de asemenea, să crească și să scadă odată cu creșterea temperaturii. Acest lucru se datorează semnului schimbării entalpiei
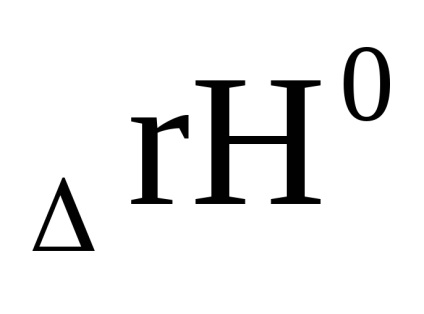
Dacă reacția directă este exotermă (