1. Cele mai simple metode de prelucrare a rezultatelor măsurătorilor multiple.
2. Metode de bază pentru detectarea și eliminarea erorilor brute și sistematice.
3. Estimări punctuale și intervale ale distribuției erorilor aleatorii.
4. Ratificarea erorilor și a formelor de reprezentare a rezultatelor măsurătorilor.
5. Reguli pentru modificarea rezultatelor măsurătorilor.
6. Estimarea erorii măsurărilor multiple directe și indirecte.
Cele mai simple metode de prelucrare a rezultatelor măsurătorilor multiple
Produs în următoarea ordine:
1. Se efectuează o măsurătoare multiplă, în urma căreia obținem valorile cantității fizice în forma:
2. Eliminăm eroarea sistematică introducând un amendament
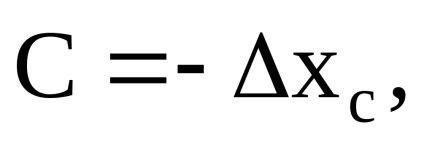
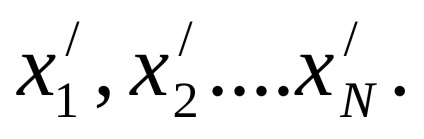
3. Calculați media aritmetică
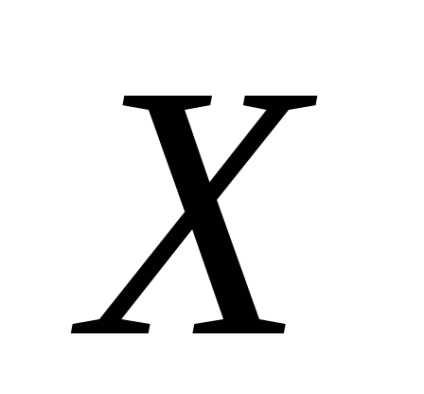
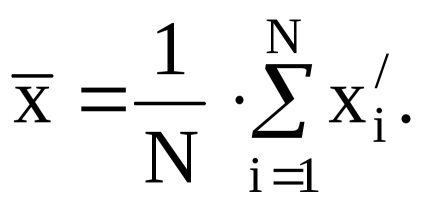
4. Calculați deviația rezultatului
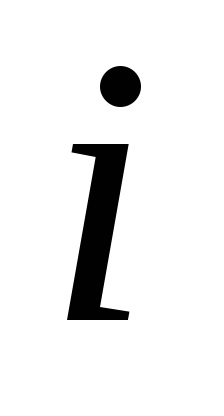
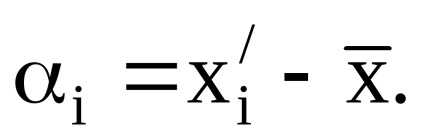
5. Calculați valoarea MSE a rezultatului măsurătorii
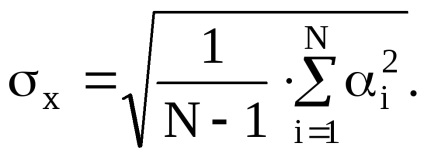
6. Estimăm normalitatea rezultatului (supravegherea) observațiilor. Pentru a face acest lucru, vom selecta cele mai mari deviații și le vom compara cu RMS:
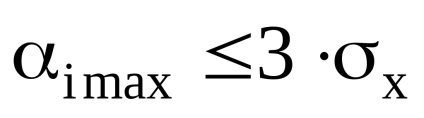
7. Dacă eroarea de măsurare este supusă legii Gauss, probabilitatea unei erori în cadrul unei deviații standard multiple σx (interval de încredere ± σx ± 2σx ± 3σx):
Scrieți rezultatul calculelor
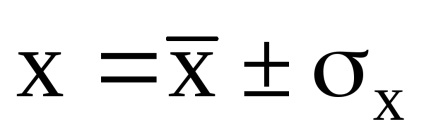
8. Dacă eroarea de măsurare este supusă legii Studentului, atunci deviația RMS a rezultatului măsurătorii:
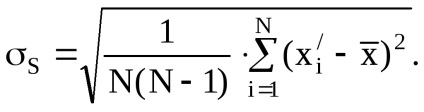
9. Calculați intervalul de încredere ε, specificând o probabilitate de încredere (de exemplu, P = 0,95). Prin valoarea și numărul de măsurători ale lui N, determinăm mai întâi prin tabel coeficientul Studentului-tS.
Valorile raportului Student în funcție de probabilitatea de încredere acceptată P și numărul de rezultate ale observațiilor n în conformitate cu tabelul. De exemplu, pentru N = 4 și P = 0,95 tS = 3,182; N = 5 la P = 0,95 tS = 2,776; pentru N = 10 tS = 2,262; n = 15 tS = 2,145 pentru același P = 0,95.
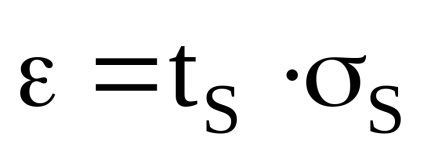
Scrieți rezultatul calculelor.
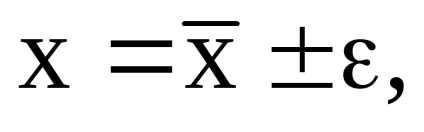
2. Metode de bază pentru detectarea și eliminarea erorilor brute și sistematice Detectarea și eliminarea erorilor brute (pierderi)
Detectarea pierderilor trebuie efectuată înainte de determinarea erorilor de măsurare. Această operație este potrivită în special în cazul în care între serii de măsurători există valori separate, foarte diferite de celelalte.
De regulă, lipsurile apar datorită acțiunilor incorecte ale operatorului, dar pot fi, de asemenea, rezultatul unei funcționări defectuoase a instrumentelor de măsurare utilizate. În toate cazurile, lipsurile nu sunt o caracteristică a măsurătorilor și pentru a evita denaturarea semnificativă a rezultatelor, ele trebuie eliminate.
Pentru o soluție obiectivă a întrebării dacă orice rezultat al măsurării este o greșeală, se folosesc metode speciale. Două dintre ele au fost cele mai utilizate pe scară largă: metoda (criteriul) 3ats și metoda tabulară (criteriul Smirnov-Grebbs).
Baza metodei 3 ("trei sigma") este presupunerea că rezultatele măsurărilor unice
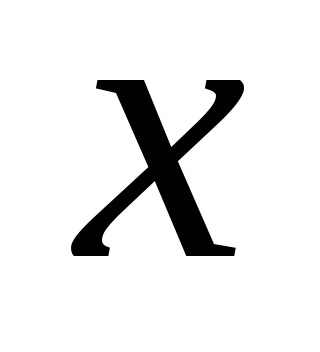
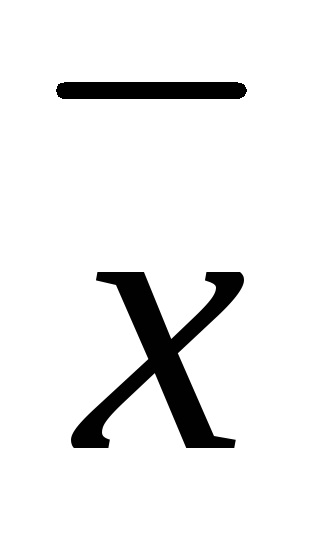
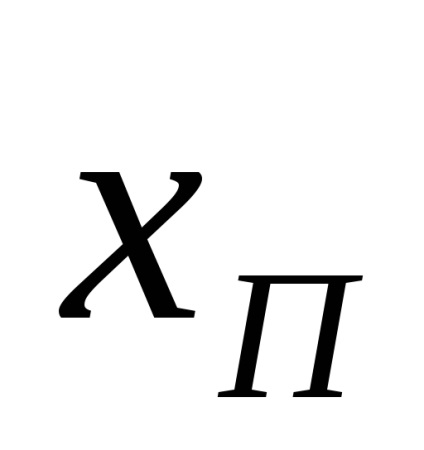
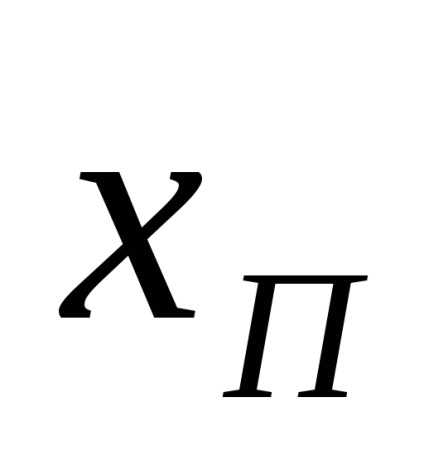
Metoda 3 este universală și poate fi utilizată pentru orice lege de distribuție a cantităților considerate. Dacă legea de distribuire a cantităților luate în considerare nu este cunoscută, atunci metoda 3 este aplicabilă oficial, dar probabilitatea de încredere cu care sunt detectate gafele rămâne necunoscută.
Pentru a detecta erorile folosind metoda 3, efectuați următoarele operații:
pentru a calcula media aritmetică a unui număr de măsurători
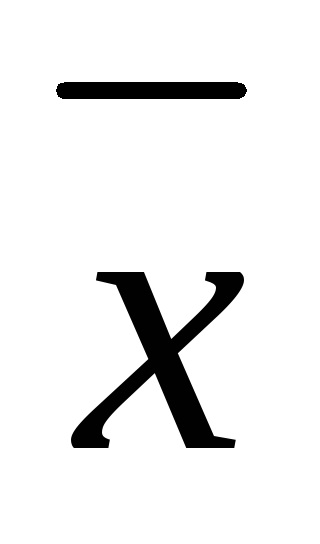
calcula deviația standard
găsiți în magnitudine absolută diferența A între valoarea asimetrică estimată xn și valoarea aritmetică medie a unei serii de măsurători.
comparați valoarea obținută de A cu 3.
Dacă condiția A <3, то величина xп не является промахом.
Dacă condiția A <3 не выполняется, то xП – промах и его следует отбросить.
Detectarea și eliminarea erorilor sistematice
Erorile sistematice ale instrumentelor de măsurare sunt, după cum sa menționat deja mai sus, componentele erorii, care într-o serie de măsurări date rămân constante sau se schimbă în mod regulat.
Trebuie remarcat faptul că erorile sistematice (ca cele aleatorii) în diferite puncte de pe scara aceluiași instrument sau dispozitiv de măsurare pot fi diferite. Prin urmare, după efectuarea cercetării, este posibil să se vorbească cu încredere în magnitudinea erorilor numai la anumite puncte ale scalei instrumentului. În ceea ce privește intervalele dintre puncte, aici se presupune că, de la un punct la altul, erorile instrumentului variază ușor (fără salturi).
Estimarea unei erori sistematice se efectuează în următoarea ordine:
în fiecare dintre punctele selectate pe scara instrumentului, media aritmetică
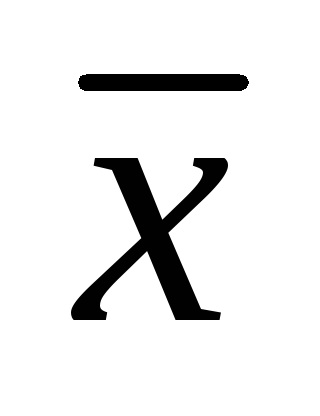
Eroarea sistematică a instrumentului de măsurare C este determinată la fiecare dintre punctele selectate ale scalei ca fiind diferența dintre media mediei aritmetice
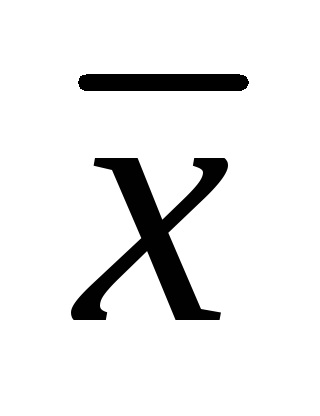
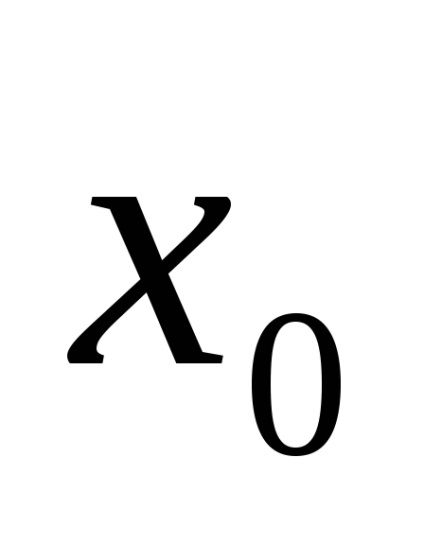
unde - este definit mai sus.
Erorile sistematice C pot fi fie pozitive (pentru
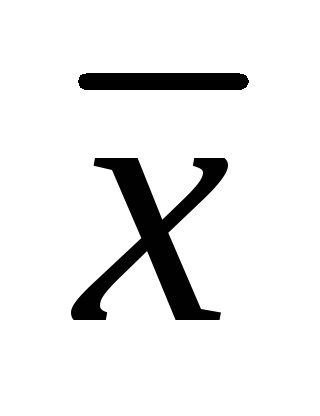
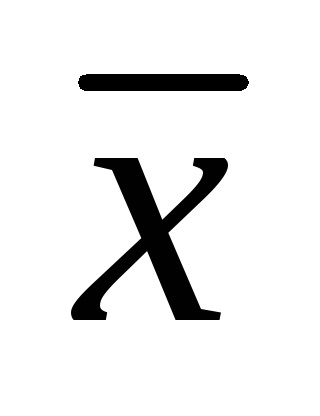
Valoarea reală a cantității măsurate x0, ca regulă, este necunoscută și în loc de x0 se folosește valoarea reală a valorii măsurate, pentru care sunt luate citirile instrumentelor standard de măsurare.
Eroarea sistematică, calculată prin formula C =
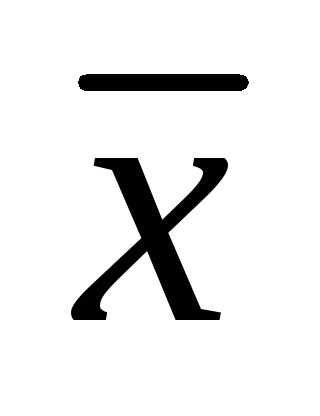
Pe lângă valorile absolute, se calculează erorile sistematice relative C și C:
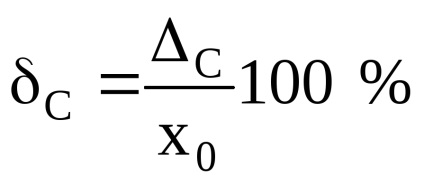
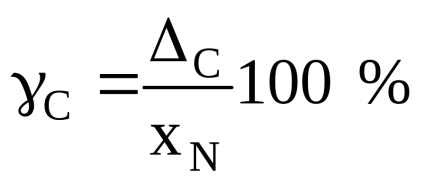
unde xN este valoarea de normalizare (în majoritatea cazurilor xN = xK);
xK este limita superioară a scalei instrumentului.
Erorile relative și reduse sunt de obicei exprimate în procente, dar pot fi exprimate și în valori relative.
În Fig. este reprezentată o axă numerică pe care este reprezentată valoarea adevărată a valorii măsurate x0 și sunt reprezentate grafic rezultatele măsurătorilor acestei cantități de către instrumentul de măsurare investigat. Ca urmare a primei măsurători, valoarea lui x1, a doua - x2, a treia - x3, etc. (rezultatele din numai primele patru măsurători sunt indicate în figură). Pe axa numerică,
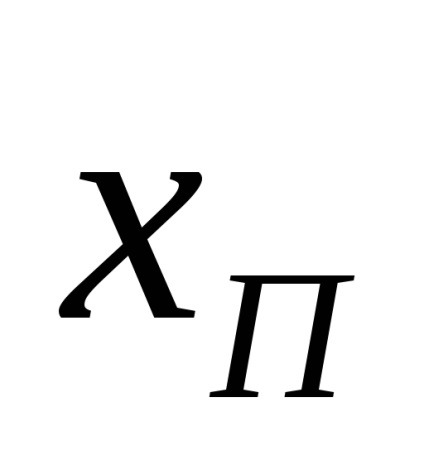
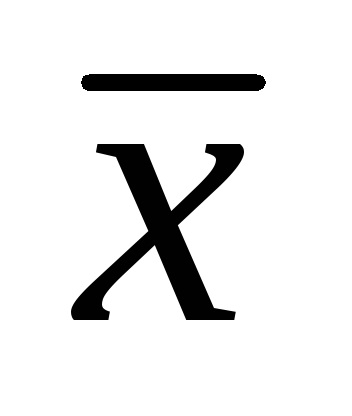

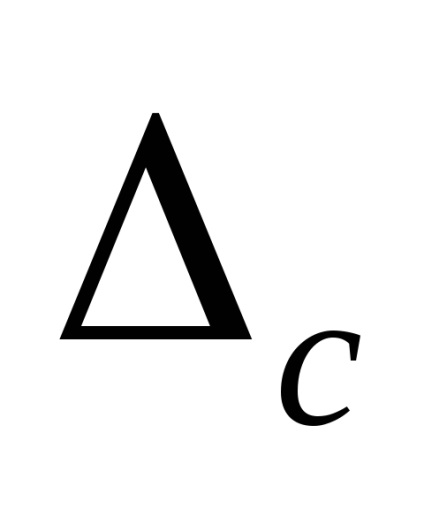


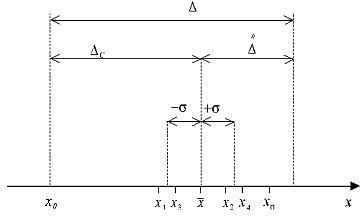
Fig. Interpretarea grafică a erorilor statice în instrumentele de măsurare.
Astfel, din figură rezultă că eroarea sistematică este o medie constantă, dar nu epuizează toate erorile dispozitivului de măsurare. Într-adevăr, diferența dintre rezultatele măsurătorilor individuale și valoarea reală a cantității măsurate poate depăși eroarea sistematică (ca, de exemplu, diferențele x2-x0 .x4-x0, etc.), adică cu excepția sistematică, eroarea este aleatorie.
Eliminarea unei erori sistematice poate fi realizată prin introducerea unui amendament la o măsurătoare a cărei mărime este egală cu valoarea absolută a erorii sistematice, iar semnul este inversul semnului acestei erori.
Pentru a elimina erorile sistematice persistente, se folosesc următoarele metode:
Metoda de compensare a erorilor prin semn. Această metodă este folosită pentru a exclude cunoscute prin natura lor, dar nu este cunoscută pentru valoarea erorilor sistematice. Măsurătorile sunt efectuate în două etape, astfel încât eroarea este inclusă în rezultatul măsurătorii cu semne opuse. La prima măsurare rezultatul este scris ca:
.
În a doua dimensiune.
Apoi, jumătate suma acestor rezultate va fi lipsită de erori sistematice și rezultatul măsurării este definit ca:
În acest fel, eroarea sistematică de la acțiunea câmpurilor magnetice externe asupra mecanismelor de măsurare este eliminată, erorile în comparatoare, circuitele de punte etc. sunt reduse.
Un exemplu. pentru a măsura EMF cu ajutorul unui potențiometru de curent continuu având o putere termică parazită. Ca urmare a unei măsurători, obținem E1. Apoi, comutarea polarității EMF măsurată, modificați direcția curentului de funcționare în potențiometru și obțineți din nou rezultatul E2.
Metoda de opoziție (modificări în semnul cantității de ieșire).
Se bazează pe posibilitatea modificării valorii de ieșire, menținând în același timp semnul și amploarea erorii sistematice.
Această metodă este utilizată pentru a compensa eroarea sistematică în SI a tipului de integrare (de exemplu, în voltmetrele digitale). Măsurătorile sunt de asemenea efectuate în două etape.
Metoda de substituire este aplicabilă dacă există o măsură ajustabilă a cărei valoare de ieșire este uniformă cu o valoare variabilă. Mai întâi, măsurați valoarea necunoscută:
Apoi, o măsură exemplară este legată de SI și se stabilește o valoare a măsurii care determină aceeași indicație a indicatorului SI.
Diferența dintre valoarea măsurată și indicatorul indicatorului SI indică o eroare sistematică. În cea mai mare măsură, această metodă este folosită pentru măsurarea R, C și L, de exemplu, utilizând circuite de bridge ale curentului alternativ.
4. Metoda de verificare. Este comună detectarea unei erori sistematice. Esența sa constă în compararea indicațiilor instrumentelor de lucru și model. Eroarea sistematică este definită ca fiind diferența în lecturi:
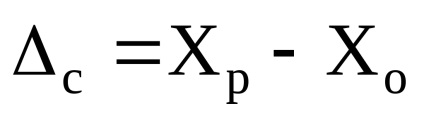
unde Xp. Ho este rezultatul măsurării de către SR de lucru și, respectiv, SI de referință. Rezultatele verificării, adică valoarea erorii sistematice este graficul corecțiilor:
Atunci când se efectuează măsurători prin acest dispozitiv, eroarea sistematică, cunoscută în magnitudine și semn, este eliminată prin introducerea unui amendament a cărui valoare numerică este egală cu valoarea erorii sistematice și opusă semnului. Corecția se introduce prin adăugarea acesteia la rezultatul măsurătorii:
,
unde Xg este rezultatul măsurării corectate.
Un nou rezultat al măsurării se numește "corectat".
Trebuie remarcat faptul că, prin utilizarea tehnologiei microprocesor și automatizarea procesului de măsurare, este posibilă corectarea automată a SI și eliminarea erorilor sistematice.
Atunci când se efectuează măsurători, se folosesc adesea metode schematice de corectare a erorilor sistematice. Includerea compensatorie a convertizoarelor, diferite circuite de corecție a temperaturii și frecvenței reprezintă exemple de implementare a acestora.
În cazurile în care există mai multe motive pentru erorile sistematice, pe baza estimărilor disponibile privind așa-numitele erori sistematice "elementare", se determină eroarea sistematică totală. În acest caz, fiecare eroare sistematică "elementară" este tratată ca o variabilă aleatoare.