Determinarea latitudinii de-a lungul înălțimii stelei polare.
Fie ca steaua polar să fie într-un punct arbitrar C. Din acest punct, să lăsăm perpendicularul sferic pe meridianul observatorului. Cantitatea x este proiecția distanței polare față de meridianul observatorului. Deoarece distanța polară este mică (44 '), triunghiul dreptunghiular PN CD poate fi considerat plat. Din acest triunghi dreptunghic au x = costm văzut din figură că = HO- x (*) Pe baza timpului de bază formule imeemx = cos (SM). Substituind în ecuația (*), valoarea x, obținem = cos (SM) furioși sunt efectuarea de notație I = - Osos (o SM) (**) o și o - valoarea medie a ascensiunii dreapta și distanțele polare Pole Star.
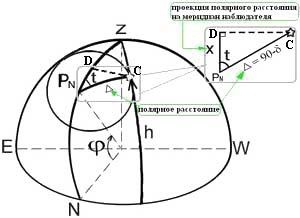
Amendamentul Eu iau în considerare rotația zilnică a stelelor în jurul valorii de Polul Nord nord a lumii, după cum se poate observa din formula (**) depinde numai de timpul sideral și este selectat din MAE „înălțime Latitudine a North Star“ tabelul de la paginile 277-278. Amendamentul II ia în considerare sfericitatea triunghiului PN CD și corectează amendamentul I, întotdeauna pozitiv, este selectat din tabelul poate „înălțimea Latitude Steaua Nordului“ la pagina 279 din argumentele cu SM și h. Amendamentul III ia în considerare schimbarea în cursul anului coordonatele ecuatoriale ale Steaua Nordului corectează amendamentul am selectat din MAE în tabelul „Amploarea înălțimea Steaua Nordului“ la pagina 280 în argumentele cu SM și data. Și pentru că toate corecțiile depind de ora locală stelar, prin urmare, pentru a determina lățimea înălțimea Steaua Nordului, în plus față de corectarea înălțimile necesare pentru a calcula timpul sideral local la acest argument, pentru a alege amendamentele I, II și III.
Ordinea observațiilor și a calculelor.
1. În crepuscul de navigație găsiți Steaua de Nord deasupra punctului N la o înălțime de h. Măsurați cu o sextantă înălțimea (OS) și observați punctul de timp de cronometru.
OC = 38 ° 40,4 'Tx = 11h 54 m 12 s