Natura transportoarelor de curent electric în metale a fost stabilită în următoarele experimente.
în. Experiențele lui Richard Tolman și colegii săi (T. Steward). 1916-1926, a dezvoltat ideile lui Mendelstamm Papaleksi și a permis obținerea primelor rezultate cantitative.
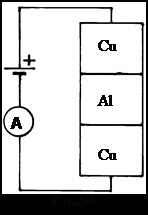
Bobina cu un număr mare de ture se rotește în jurul axei sale și apoi fusese frânată brusc. Capetele firului bobinei ar putea fi răsucite și atașate la un galvanometru balistic. Câmpul magnetic al pământului a fost compensat cu atenție de conductori cu curent. Cu o frânare ascuțită a bobinei, galvanometrul a cedat.
Dacă m - masa inerțială purtătorilor de sarcină electrică, și e sunt sarcina lor, schimbarea în impulsuri de frânare purtătorilor de sarcină egală cu (mN) dv = Fdt = (eN) Edt (9.1)
Aici N este numărul de suporturi de încărcare în volumul sârmei bobinei.
Împărțirea cu N și luând în considerare faptul că E = Uçl. unde U este tensiunea la capetele firului, iar l este lungimea sa, iar U = Ri; unde R este rezistența circuitului și i este curentul care circulă în circuit, obținem o modificare a impulsului purtătorului de încărcare unitar.
După integrarea peste timpul de frânare al bobinei, obținem:
Viteza de rotație liniară a fost v = 300 m / s, lungimea sârmei bobinei este l = 500 m. Experimente cu fire din cupru, aluminiu, argint. La rezistențele diferite ale circuitului R și ale diferitelor valori ale încărcării g măsurate de galvanometru, sarcina specifică a purtătorilor sa dovedit a fi aceeași și egală cu eçm = 1,6 x 10 11 Cl / kg. Acest lucru a fost aproape de rezultatele obținute de J. Thomson cu douăzeci de ani mai devreme în experimente cu raze catodice.
Generalizarea rezultatelor răspunsurilor de mai sus ne-a permis să tragem următoarele concluzii:
Purtătorii încărcăturilor electrice în toate metalele sunt identice;
Purtătorii încărcăturilor electrice din metale sunt destul de materiali, inerțiali și slabi legați de grâul de cristal al metalului:
Taxa specifică a transportatorilor este eçm = 1,6 x 10 11 Cl / kg.
Deoarece în această perioadă (sfârșitul anilor 20 ai secolului XX) Milliken a determinat încărcarea elementară e = 1,6 × 10 -19 Cl, a fost posibil să se estimeze masa inerțială a transportatorilor. .
Purtătorii actuali din metale erau electroni detectați mai devreme în raze catodice (1897) și un nor termionic de metale de sodiu. (1988, T. Edison).
În general, conductivitatea electrică trebuie considerată ca un fenomen al transferului materiei și al încărcăturii electrice. Legea determinantă în acest din urmă caz este legea lui Ohm.
2.Tectiva electronică a conductivității metalelor. În primul deceniu al secolului XX, Paul Drude și Hendrik Lorenz au construit o clasică, adică, bazată pe teoria electronică a ecuației Maxwell a conductivității metalelor.
Ei au pornit de la ipoteza că electronii de valență din metale sunt atât de slabi conectați la atomii lor, încât ei se pot mișca cu ușurință de la un atom la altul numai în detrimentul energiei mișcării termice. Un astfel de set de electroni de valență a fost interpretat de ei ca un gaz de electroni, care respectă statica lui Maxwell Boltzmann și este ideal în proprietățile sale.
Natura ideală a gazului de electroni înseamnă că electronii de conducere nu se ciocnesc, se ciocnesc numai cu locurile de zăbrele și se află în echilibru termic cu ei. Din această condiție, putem estima viteza medie termică a electronilor
Luați în considerare, după cum se explică prin teoria conducerii Drude-Lorentz, legile Ohm și Joule-Lenz. Pentru a simplifica estimările, presupunem că toți electronii de conducere au aceeași viteză de mișcare termică, U.
a. Legea lui Ohm. Dacă creați un câmp E în interiorul metalului. atunci o mișcare haotică a electronilor este suprapusă printr-o mișcare orientată spre o viteză medie de derivație v. Curentul care curge în conductor prin secțiunea transversală a lui S. este I = enSv. unde n este concentrația electronilor de conducere, e este sarcina lor. Densitatea curentului. (9.5)
Să găsim viteza medie de deviație v. Presupunem că electronul aflat sub acțiunea forței eE în intervalul de timp t de la o coliziune cu cel al rețelei la celălalt se deplasează cu accelerația a și crește viteza ei de la 0 la. (9.6)
Deoarece mișcarea unui electron într-un câmp electric este accelerată uniform, viteza medie este jumătate din valoarea maximă; , (9,7)
și densitatea curentului este. (9.8)
Formula (9.8) exprimă legea lui Ohm în formă diferențiată în teoria electronilor. Coeficientul înainte ca E să descifreze caracteristica macroscopică a conductorului, conductivitatea specifică g prin setul de micro-caracteristici ale gazului de electroni.
Să estimăm timpul mediu t al traiectoriei medii libere a electronilor de conducere prin exemplul de cupru. Credem că există un electron liber pe atom de cupru. Dacă M este masa molară a cuprului, d este densitatea sa, apoi concentrația electronilor liberi. Înlocuind n în expresia conductivității.
În intervalul de timp t între două coliziuni, electronul călătorește o distanță medie, ceea ce înseamnă câteva zeci de atomi transversali.
Să estimăm viteza medie de derivație v a electronilor de conducere din cupru la o intensitate a câmpului E = 0,1 Vç m. Din formula (9.7) obținem:
Viteza de deviație este de un miliard de ori mai mică decât viteza termică u = 10 5 m / s.
Rețineți că tensiunea E = 0,1 V / m nu este atât de mică cât pare. Aceasta corespunde unei tensiuni de 0,1 V la capetele firului de 1 m. La această tensiune, un curent trece printr-un fir de cupru de secțiune transversală S = 1 mm2.
b. Legea lui Joule-Lenz. Masa electronilor este mai mult de o mie de ori mai mică decât masa atomilor din locurile de zăbrele. Prin urmare, pentru o coliziune inelastică cu un nod, electronul se oprește, viteza lui ajunge la 0, iar energia cinetică de deviere este dat complet nodului. Deoarece în momentul coliziunii (formula 9.6), energia dată de electroni pe unitatea de volum într-o secundă este egală cu
Această energie este eliberată sub formă de căldură, prin urmare formula (9.9) exprimă legea lui Joule Lenz într-o formă diferențială. Expresia pentru conductivitate (9.10)
rezultatul este același ca în formula legii lui Ohm (9.8).
Strict vorbind, presupunerea că electronul renunță la toate energiile într-o coliziune cu un atom este valabil numai atunci când atomul este în repaus. Dar atomii vibrează și coliziunile nu sunt absolut inelastice. Prin urmare, electronii pot da atat energia (coliziune cu un atom care se sustrage), cat si a lua-o (coliziuni cu un atom care intra). În statisticile în condiții de echilibru termic, energia medie a mișcării electronilor la temperatură constantă rămâne constantă.
Dar, când gazul electronic dobândește o viteză de deviație direcțională, acesta obține o surplus de energie peste energia termică a mișcării. Această energie de electroni nu este echilibrată cu energia nodurilor. Prin urmare, este transferat continuu către nodurile rețelei cristaline, crescând temperatura conductorului.
în. Legea Wiedemann Franz. În 1853 germanii G.Vedemann și R.Francz au stabilit că raportul dintre conductivitatea termică c și conductivitatea electrică g la aceeași temperatură este același pentru toate metalele. În 1882, fizicianul danez Ludwik Lorenz a arătat că acest raport este proporțional cu temperatura absolută a legii Wiedemann-Franz. (9.11)
Aici L este un coeficient care este același pentru toate metalele, se numește numărul Lorentz.
Teoria electronică clasică explică această lege în acest fel.
Deoarece electronii sunt foarte mobili, se poate presupune că conductivitatea termică a metalelor se datorează în principal conductivității termice a gazului său de electroni. Conductivitatea termică este (9.12)
Aici l este calea medie liberă a electronilor, u este viteza lor medie de mișcare termică, i = 3 este numărul de grade de libertate a electronilor, k este constanta Boltzmann.
Înlocuind c din (9.12) și g din (9.10) în formula (9.11), unde t = lçu. obținem: (9.13).
Din teoria cinetică a gazelor ideale, viteza medie a mișcării termice a electronilor este U 2 = 8 kTçpm. De aici (9.14).
Teoria electronică clasică în ansamblu interpretează corect legea lui Wiedemann Franz. Se descifrează numărul Lorentz L = 8k 2 çpm ca o combinație de constante și prezice o relație liniară între cçg pe temperatura T.
4. Dificultăți ale teoriei electronice clasice. Concluziile de mai sus se datorează lui Drude și au fost făcute de el presupunând că toți electronii de conducere au aceeași viteză u a mișcării lor termice.
Henryk Lorenz a rafinat concluziile prin adoptarea distribuției vitezelor de electroni de către Maxwell. Ca urmare, în formula Wiedemann Franz, coeficientul de 8çp = 2,55 a devenit exact 2. Cu toate acestea, formula rafinată a devenit inferioară experienței.
Capacitatea termică molară a metalelor ar trebui să fie compusă din capacitatea de căldură a zonelor de zăbrere 3R și căldura specifică a unui gaz electron ideal 3Rzç 2, unde z este numărul de electroni de valență la atom. Capacitatea totală de căldură este obținută ca 3R + 3Rzç 2. Dar experiența oferă capacitatea de căldură a 3R (Legea lui Dulong și Petit). Teoria clasică nu explică acest lucru.
În formula de conductivitate specifică g = ne 2 l / 2mu, valoarea vitezei medii u în conformitate cu teoria statistică a gazelor ideale este proporțională cu rădăcina pătrată a temperaturii. Deoarece, atunci u
. Prin urmare, g = 1çr
. Dar experiența oferă o dependență liniară a rezistivității de temperatura, sau r
T. Discrepanța este inexplicabilă.
Teoria electronică clasică este complet incapabilă să explice fenomenul de superconductivitate. Esența lui este că, la o anumită temperatură, numită Tc critică și aproape de zero absolut în majoritatea metalelor pure chimic, rezistivitatea conductorului scade brusc la aproape zero. Să estimăm, realizat în timp de atenuare a unui curent într-un inel supraconductor, arată că rezistivitatea supraconductorilor nu este mai mare de 10-25 ohm × m. Pentru comparație, rezistivitatea cuprului în starea convențională este de 1,7 x 10 -8 Ω × m.
În teoria electronilor clasici, r
, rezistivitatea ar trebui să scadă monoton cu temperatura, nu există salt.
5. Limitele aplicabilității teoriei electronilor. Teoria clasică a conductivității electrice a solidelor este cu atât mai divergentă cu experimentul, cu atât este mai mică temperatura conductorului și cu atât este mai mare concentrația de electroni de conducere. În acele cazuri când temperatura este suficient de mare, T> Tcom. și concentrația purtătorilor este mică, utilizarea teoriei electronilor este justificată nu numai pentru estimări calitative, ci și pentru estimări cantitative. Aceasta este o posibilitate foarte valoroasă, deoarece teoria electronică clasică a Drude-Lorentz este mult mai simplă și mai intuitivă decât teoria electronică cuantică.
Înapoi la cuprins: