Prezentare pentru lecție
Scopul lecției este de a examina trăsăturile unui paralelogram și de a consolida cunoștințele dobândite în procesul de rezolvare a problemelor.
obiective:- educație: formarea abilităților de a aplica semne de paralelogram pentru rezolvarea problemelor;
- dezvoltarea: gândirea logică, atenția, aptitudinile de auto-studiu, aptitudinile de autoevaluare;
- educație: educația de interes pentru subiect, abilitatea de a lucra într-o echipă, o cultură a comunicării.
Tipul lecției: învățarea materialului nou, fixarea primară.
Echipamente: tablă interactivă, proiector, cărți cu sarcină, prezentare.
1. Moment organizatoric.
U: Bună ziua, băieți! Astăzi la lecție vom vorbi din nou despre paralelogramă. Trebuie să îndeplinim multe sarcini, să dovedim teoremele și să învățăm cum să le aplicăm în rezolvarea problemelor. Motto-ul lecției noastre va fi cuvintele lui Le Carbusier: "Totul este geometria".
2. Actualizarea cunoștințelor studenților.
Unii elevi dau sarcini individuale pe cărțile de pe proprietățile unui paralelogram (setare selectează fiecare în mod independent, o prezentare de diapozitive pe hyperlink, punând cursorul mouse-ului pe forma, dar nu un număr). ascultați individual fiecare respondent.

Cu restul, dovedim proprietăți suplimentare ale paralelogramului. (Mai întâi discutați dovezile orale, apoi verificați cu tabla interactivă).
1 °. Bisectorul unghiului paralelogramului taie un triunghi izoscel din el.
2 °. Bisectoarea unghiurilor adiacente ale unui paralelogram sunt perpendiculare, iar bissektrisyprotivopolozhnyh unghi paralel sau coliniare.
După pregătire, ascultați dovada proprietăților suplimentare ale paralelogramului.
AE este bisectorul unghiului BAD.
Dovedeste: ABE este isoscele.
Din moment ce ABCD este o paralelogramă, înseamnă că BC || AD, apoi unghiul EAD = unghiul BEA ca fiind transversal cu liniile paralele BC și AD și secvența AE. AE este bisectorul unghiului BAD, prin urmare, unghiul BAE = unghiul EAD, astfel încât unghiul este BAE = unghiul BEA.
În ABE, unghiul este BAE = unghiul BEA, deci ABE este isoscele cu baza AE.
Formulează semnul unui triunghi isoscel.
Ce unghiuri în BAE pot fi egale? De ce?
BE este bisectorul unghiului CBA,
AE este bisectorul unghiului BAD.
Când vor fi liniile AE și CK paralele?
Sunt unghiurile BEA și <3? Почему?
În ce caz va coincide AE și CK?
Pregătire pentru învățarea unui material nou
Lucrul frontal cu clasa (oral).- Ce înseamnă "proprietăți" și "semn"? Dați exemple.
- Care este teorema inversă?
- Declarația este întotdeauna inversă? Dați exemple.
3. Explicarea noului material.
U. Fiecare obiect are propriile proprietăți și atribute. Spuneți-mi, vă rog, decât proprietățile diferă de caracteristici.
Să încercăm să înțelegem această întrebare pe un exemplu simplu. Obiectul dat este toamna. Denumiți proprietățile sale: Semnele sale:

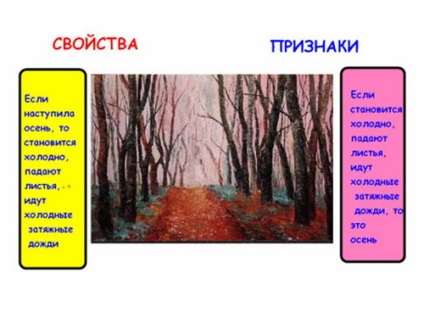
- Care sunt afirmațiile despre proprietate și semnul obiectului în raport unul cu celălalt? (răspuns: invers)
- Ce proprietăți am studiat în cursul geometriei? Formeaza-le. (numit mai multe)
Este posibil să construiți o declarație adevărată inversă pentru orice proprietate? (răspunsuri diferite).
Să o verificăm pe următoarele proprietăți:
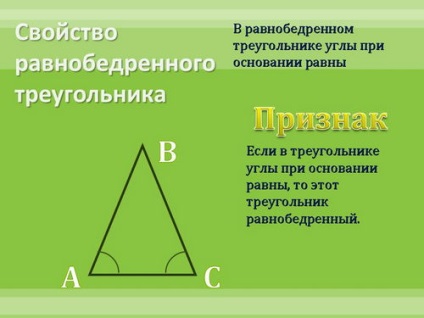
Concluzionați: pentru orice proprietate, puteți construi o declarație converse potrivită? (nu, nu pentru nimeni)
Acum, să ne întoarcem la quadrangle, să ne amintim proprietățile sale și să formulăm declarații inverse pentru ei, adică (răspunsul este semnele unui paralelogram). Deci, tema lecției de astăzi: "Atributele unei paralelograme".
Deci, care sunt proprietățile paralelogramului?
Menționați proprietățile inverse ale instrucțiunii. (elevii formulează semnele, profesorul le corectează și le formulează din nou)
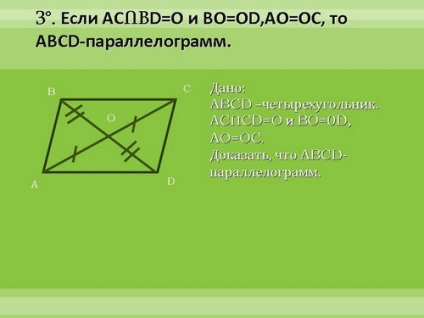
Să dovedim aceste semne. Primul semn - în detaliu, al doilea - în curând, al treilea - independent la domiciliu.

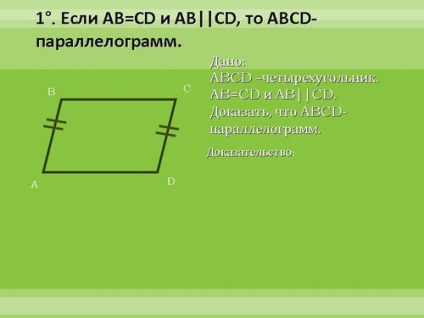
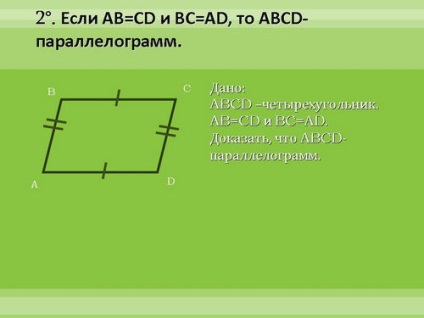
4. Securizarea materialului studiat.
Lucrați în cărți de lucru: rezolvați sarcina numărul 11 pe tabla interactivă de tablă pentru a provoca un elev mai puțin pregătit.
Soluția problemei № 379 (decizia de a scrie pe tabla interactivă). Din vertexele B și D ale paralelogramelor ABCD, unde AB BC și A sunt ascuțite, se trasează perpendiculele VC și DM pe linia dreaptă AC. Dovedeste ca BMDK patrulaterala este o paralela.
Îi dau timp elevilor să pregătească un desen.
Dată: ABCD - paralelogramă, BK AC, DM
Dovedeste-o. că: BMDK este o paralelă.
BKC = DMA pe ipotenuza și un unghi ascuțit (ca o cruce situată unghiuri de linii paralele AD și BC și AC intersectându, BC = AD ca partea opusă a paralelogramului, BKC și DMA dreptunghiular), apoi MD = BK.
BMK și DKM - dreptunghiular, BMK = DKM două Catete (picior comun MD = BK, KM), apoi BM = DK.
În cvadrantul BMDK, părțile opuse sunt egale (MD = BK și BM = DK), prin urmare, BMDK este o paralelogramă.
5. Soluția independentă a sarcinilor (sarcinile sunt alese de studenți pe tabla interactivă, decizia este verificată de consiliu, făcând clic pe hyperlink)
Înapoi la selecția de sarcini, puteți reveni prin hyperlink.
6. Rezultatul lecției. Trimiterea în casă.
Deci, să rezumăm lecția de astăzi. Răspundeți la întrebările mele:- Care sunt afirmațiile despre proprietate și semnul obiectului în raport unul cu celălalt?
- Formulează semnele unui paralelogram?
- De ce avem nevoie de o paralelogramă?
Tema: paragraful 43, dovada celui de-al doilea și al treilea semnal de terminat, nr. 380, nr. 383.
U. Băieți, am studiat astăzi semnele paralelogramului, le-am dovedit și vreau să știu cum ați înțeles materialul lecției? (lăsați banda necesară pe desktop)