Programare dinamică
Caracteristica principală a algoritmilor "divide și conquer", considerată în secțiunea 5.2, este împărțirea problemei în subprobleme independente. Dacă subtaskele nu sunt independente, situația devine mai complicată, în primul rând deoarece implementarea imediată recursivă a celor mai simpli algoritmi de acest tip poate necesita cheltuieli inacceptabile de timp. Această secțiune analizează o abordare sistematică care evită acest pericol în unele cazuri.
De exemplu, programul 5.10 este o implementare directă recursivă a relației de recurență definind numerele Fibonacci (vezi "Structurile de date elementare"). Nu folosiți acest program - este foarte ineficient. Într-adevăr, numărul apelurilor recursive pentru calculul FN este FN + 1. Dar FN este aproximativ egal cu N. f unde f „1618 -.... Proporția secțiunii de aur Surprinzător, dar pentru programul de 5.10 ori acest calcul elementar este determinat de dependența exponențială Figura 5.14 care arată apelurile recursive un mic exemplu, este clar demonstrată de cerute numărul de calcule repetate.
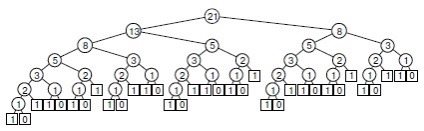
Fig. 5.14. Structura unui algoritm recursiv pentru calculul numerelor Fibonacci
Din schema apelului recursiv pentru calculul F8 folosind algoritmul recursiv standard, puteți vedea cum o recursie cu sub-sarcini suprapuse poate duce la o creștere exponențială a costurilor. În acest caz, al doilea apel recursiv ignoră calculul efectuat în timpul primului apel, ceea ce conduce la recalculații semnificative, deoarece efectul crește exponențial. Apelurile recursive pentru calculul lui F6 = 8 (arătate în subruiul drept al rădăcină și în subordonatul din stânga al subrubricii stângi a rădăcinii) sunt prezentate mai jos.

În schimb, folosind o matrice obișnuită, puteți calcula cu ușurință primele numere N Fibonacci într-un timp proporțional cu N:
Numerele cresc exponențial, astfel încât matricea să nu fie mare; de exemplu, F45 = 1836311903 este cel mai mare număr Fibonacci, care poate fi reprezentat de un număr întreg de 32 de biți, deci este suficient să folosiți o matrice cu 46 de elemente.
Această abordare oferă o cale imediată de a obține soluții numerice pentru orice relație de recurență. În cazul numerelor Fibonacci, se poate face fără nici măcar o matrice și se limitează doar la ultimele două valori (a se vedea Exercițiul 5.37); Cu toate acestea, în multe alte cazuri de relații de recurență care apar frecvent (a se vedea, de exemplu, Exercițiul 5.40), este necesară o matrice pentru stocarea tuturor valorilor cunoscute.
Programul 5.10. Numerele Fibonacci (implementare recursivă)
Acest instrument arată compact și elegant, dar inaplicabile în practică, deoarece timpul de calcul depinde exponențial pe FN N. Timpul de calcul FN + 1 f „de 1,6 ori mai mare FN de calcul. De exemplu, deoarece f 9> 60, în cazul în care computerul pentru a calcula necesară Fn aproximativ o secundă, atunci este nevoie de mai mult de un minut pentru a calcula FN + 9 și mai mult de o oră pentru a calcula FN + 18.
O relație de recurență este o funcție recursivă cu valori întregi. Argumentele prezentate în paragraful precedent, sugerează că orice astfel de funcție poate fi calculată prin calcularea valorilor tuturor, începând cu cel mai mic, iar la fiecare pas folosind valorile calculate anterior pentru a calcula valoarea curentă. Această tehnică se numește programare dinamică de jos. Se aplică pentru orice calcul recursiv, cu condiția să se poată stoca toate valorile calculate anterior. Această tehnică de dezvoltare a algoritmilor este utilizată cu succes pentru a rezolva o gamă largă de probleme. Așadar, acordați atenție acestei tehnologii simple, care poate schimba timpul de execuție al algoritmului de la exponențial la linear!
programare dinamică descendentă (top-down programare dinamică) - chiar și tehnica mai simplă, care vă permite să realizați în mod automat funcții recursive cu aceeași (sau mai mici), numărul de iterații ca programarea dinamică în amonte. Atunci când acest program este recursiv (acțiune de închidere) stoca fiecare valoare calculată și s (prima acțiune) să verifice aceste valori pentru a se evita recalcularea oricare dintre ele. Programul 5.11 este rezultatul conversiei mecanice a programului 5.10, în care programarea dinamică descendentă a permis reducerea timpului de execuție la liniar.
În Fig. 5.15 demonstrează o scădere radicală a numărului de apeluri recursive obținute prin această simplă schimbare automată. Uneori, programarea dinamică descendentă se numește și memoizare.
Ca un exemplu mai complex, ia în considerare problema rucsacul: un hoț jefuit un seif l N tipuri de obiecte de diferite dimensiuni și valoare găsește, dar are doar o mică capacitate rucsac M, pentru care poate transporta prada. Sarcina este de a determina combinația de obiecte pe care hoțul trebuie să le împacheteze în rucsac, astfel încât valoarea totală a bunurilor furate să fie mai mare.
Programul 5.11. Numerele Fibonacci (programare dinamică)
Salvarea valorilor calculate într-o matrice statică (ale cărei elemente sunt inițializate la 0 în C ++) face posibilă excluderea explicită a oricăror recalculații. Acest program calculează Fn într-un timp proporțional cu N, care diferă semnificativ de timpul 0 (φ N), care este necesar pentru calculele programului 5.10.
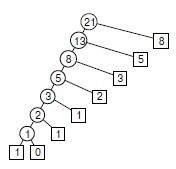
Fig. 5,15. Aplicarea programării dinamice descendente pentru a calcula numerele Fibonacci
Din această schemă de apeluri recursive efectuate pentru a calcula F 8 în jos prin programare dinamică, poate fi văzută ca păstrarea valorilor calculate reduce costurile cu exponențială (vezi. Fig. 5.14) la o liniară.
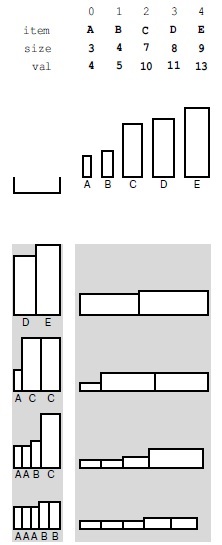
Fig. 5.16. Un exemplu de problemă rucsac
Intrare problema rucsacului date (de mai sus) sunt capacitate și ranițe un set de obiecte de dimensiuni diferite (care sunt reprezentate de valorile de pe axa orizontală) și valoarea (valoarea pe axa verticală). Această figură prezintă patru moduri diferite de umplere a unui rucsac, al cărui mărime este de 17; două dintre aceste metode dau o valoare maximă totală de 24.
De exemplu, în prezența tipurilor de obiecte prezentate în Fig. 5.16. Un hoț cu un rucsac, al cărui mărime este de 17, poate să ia doar cinci (dar nu șase) articole A cu o valoare totală de 20 sau articole D și E cu un cost total de 24 sau una din numeroasele combinații. Scopul nostru este de a găsi un algoritm eficient pentru determinarea soluției optime pentru orice set de obiecte și capacitatea rucsacului.
Soluțiile problemei rucsacului sunt importante în multe aplicații. De exemplu, o companie de transport poate avea nevoie să determine cea mai bună modalitate de încărcare a unui camion sau a unei aeronave de transport. În aplicații similare, pot exista alte variante ale acestei sarcini: de exemplu, numărul elementelor fiecărei specii poate fi limitat sau pot fi disponibile două camioane. Multe dintre aceste opțiuni pot fi rezolvate folosind aceeași abordare care va fi luată în considerare mai jos pentru rezolvarea problemei de bază doar formulate, dar există și variante mult mai complicate. Există o linie fină între problemele rezolvate și insolvabile de acest tip, dar acest lucru va fi discutat în partea 8.
În soluția recursivă a problemei rucsacului pentru fiecare alegere a unui obiect, presupunem că putem determina (recursiv) modul optim de a umple spațiul rămas în rucsac. Dacă volumul rucsacului este egal cu capacul, atunci pentru fiecare element disponibil i este determinat costul total al elementelor, care ar putea fi realizat prin plasarea elementului i în rucsac cu împachetarea optimă a elementelor rămase. Această împachetare optimă este pur și simplu un pachet care este definit (sau va fi definit) pentru un rucsac mai mic cu capacul volumului - numere [i] .size. Aici este folosit următorul principiu: deciziile optime luate în viitor nu necesită revizuire. Când se determină cum să se împacheteze în mod optim dimensiuni mai mici, aceste sarcini nu necesită reexaminare, indiferent de următoarele elemente.
Programul 5.12 este o soluție direct recursivă, care se bazează pe raționamentul de mai sus. Acest program este, de asemenea, inaplicabil pentru rezolvarea problemelor reale, din cauza numărului mare de calcule repetate (vezi Figura 5.17), timpul de decizie este legat de numărul de elemente exponențial. Dar pentru a rezolva problema, puteți utiliza în mod automat programarea dinamică de sus în jos - și obțineți programul 5.13. Ca și înainte, această tehnică exclude toate recalculațiile (a se vedea figura 5.18).
Programul 5.12. Problema rucsacului (realizarea recursivă)
Ca și în cazul calculului recursiv al numerelor Fibonacci, nu utilizați acest program, deoarece va dura un timp exponențial pentru executarea acestuia și, prin urmare, este posibil să nu fie posibilă obținerea unei soluții chiar pentru o sarcină mică. Cu toate acestea, programul prezintă o soluție compactă care poate fi ușor îmbunătățită (a se vedea programul 5.13). Se presupune că elementele sunt structuri cu dimensiune și valoare, care sunt definite ca
și există o serie de elemente N de element de tip. Pentru fiecare element posibil, valoarea maximă care poate fi obținută (recursiv) se calculează prin includerea acestui element în eșantion și apoi se selectează maximul tuturor valorilor.
Programul 5.13. Problema rucsacului (programare dinamică)
Această modificare mecanică a programului 5.12 reduce timpul de execuție de la exponențial la liniar. Noi pur și simplu stoca orice valoare calculată a funcției și apoi, în loc să efectuăm apeluri recursive, vom selecta valorile salvate atunci când sunt necesare (folosind un semn special pentru a reprezenta valori necunoscute). Indicele se menține, cu toate acestea, dacă se dorește, se poate restaura întotdeauna conținutul rucsacul după calcul: itemKnown [M] este într-un rucsac, alt conținut coincide cu optimă dimensiune de ambalare rucsac M -itemKnown [M]. dimensiunea, prin urmare, în rucsac este itemKnown [M-litere [M] .size], etc.
Fig. 5.17. Structura recursivă a algoritmului pentru rezolvarea problemei rucsacului
Acest arbore reprezintă structura apelurilor recursive a unui algoritm recursiv simplu pentru rezolvarea problemei rucsacului realizat în programul 5.12. Numărul din fiecare nod înseamnă spațiul liber rămas în rucsac. Un dezavantaj al algoritmului este același runtime-exponențială de la -acest volum mare de calcule repetate necesare pentru soluție de suprapunere subproblemelor care în calculul numerelor Fibonacci (vezi. Fig. 5.14).
Fig. 5.18. Aplicarea metodei programării dinamice de sus în jos pentru implementarea algoritmului de rezolvare a problemei rucsacului
Ca și în cazul calculării numerelor Fibonacci, tehnica de conservare a valorilor cunoscute reduce costul algoritmului de la exponențial (vezi Figura 5.17) la liniar.
Programarea dinamică exclude în mod fundamental toate recalculațiile din orice program recursiv, cu condiția să se poată stoca valorile funcțiilor pentru argumentele mai mici decât argumentul apelului curent.
LEMMA 5.3. Programarea dinamică reduce timpul de execuție al unei funcții recursive la cel mult timpul total necesar pentru a calcula o funcție pentru toate argumentele mai mici sau egale cu un argument dat, cu condiția ca costurile unui apel recursiv să fie constante.
Vezi exercițiul 5.50.
Așa cum se aplică la problema rucsacului, rezultă din lema că timpul de execuție este proporțional cu produsul NM. Astfel, problema rucsacului poate fi rezolvată cu ușurință atunci când capacitatea rucsacului nu este foarte mare; Pentru capacități foarte mari, timpul și memoria cerute pot fi prohibitiv mari.
Programarea dinamică ascendentă se aplică și problemei rucsacului. -Asta toate metodă, în toate cazurile, puteți aplica metoda de programare în creștere atunci când programarea pe legătură în jos se aplică numai atunci când este necesar să se asigure că calculul valorilor în ordinea corespunzătoare, pentru fiecare valoare a fost calculată atunci când aveți nevoie. Pentru funcții cu doar un singur argument întreg, cum ar fi discutat, puteți efectua calcule pur și simplu, în ordinea argumentului (a se vedea. Exercitiul 5.53), dar pentru funcții recursive mai complexe care determină ordinea corectă poate fi o provocare.
De exemplu, nu este necesar să vă limitați la funcții recursive cu un singur argument întreg. Dacă există o funcție cu mai multe argumente întregi, soluțiile de subprobleme mai mici pot fi stocate în matrice multidimensionale, o dimensiune pentru fiecare argument. În alte situații, se poate renunța total la argumentele întregului și se folosește formularea discretă abstractă a problemei, ceea ce face posibilă împărțirea problemei în mai puțin complexe. Exemple de astfel de probleme sunt considerate în părțile V-VIII.
Dacă utilizați programarea dinamică descendentă, valorile cunoscute sunt păstrate; Când se utilizează programarea dinamică din amonte, acestea sunt calculate în avans. În general, programarea dinamică descendentă este preferabilă programării ascendente, deoarece
- reprezintă o transformare mecanică a soluției naturale a problemei;
- ordinea de rezolvare a sub-sarcini este determinată de ea însăși;
- Este posibil să nu fie necesar să rezolvați toate subtaskele.
Aplicațiile care utilizează programarea dinamică diferă în funcție de natura subtask-urilor și de cantitatea de informații stocate pentru ele.
Cu toate acestea, vă rugăm să rețineți următorul punct important: programarea dinamică devine ineficientă atunci când numărul de valori posibile ale unei funcții care poate fi necesară este atât de mare, încât nu ne putem permite să le păstreze (într-o programare în jos) sau pentru a calcula în avans (la o programare ascendentă). De exemplu, dacă în problema unui rucsac volumul rucsacului și dimensiunile elementelor sunt numere pe 64 de biți sau în virgulă mobilă, valorile nu pot fi salvate prin indexarea acestora în matrice. Acest lucru nu este doar un mic inconvenient, este o dificultate fundamentală. Nu există soluții acceptabile pentru astfel de sarcini; după cum se va vedea în partea a 8-a, există motive întemeiate să credem că nu există nicio soluție eficientă.
Programarea dinamică este o tehnică de dezvoltare a algoritmilor care este concepută în primul rând pentru a rezolva probleme complexe de tipul celor care vor fi luate în considerare în părțile V-VIII. Cele mai multe dintre algoritmi discutate în părțile II - IV, este o punere în aplicare a metodelor de „divide și cuceri“ la non-se suprapun sub-probleme, și sa concentrat asupra creșterii mai Subquadratic sau performanța subliniară decât subexponential. Totuși, programarea dinamică descendentă este tehnica de bază pentru realizarea realizărilor eficiente ale algoritmilor recursivi, care este prezentă în arsenalul de fonduri al oricui participă la crearea și implementarea algoritmilor.