A. Einstein a pus bazele teoriei speciale a relativității (STR). Această teorie este o teorie fizică modernă a spațiului și a timpului, în care, ca și în mecanica clasică newtoniană, se presupune că timpul este omogen, iar spațiul este omogen și izotrop. Teoria specială a relativității este adesea numită și teoria relativistă. iar fenomenele specifice descrise de această teorie sunt efecte relativiste.
Baza teoriei speciale a relativității este postulatele lui Einstein. formulată de el în 1905.
I. Principiul relativității: nici o experiență (mecanice, electrice, optice), realizat într-un cadru inerțial dat de referință, fac imposibilă pentru a detecta dacă sistemul este în repaus sau se deplasează uniform într-o linie dreaptă; toate legile naturii sunt invariabile în ceea ce privește tranziția de la un cadru de referință inerțial la altul.
II. Principiul invarianței vitezei luminii: viteza luminii într-un vid nu depinde de viteza mișcării unei surse de lumină sau de un observator și este aceeași în toate cadrele inerțiale de referință.
Primul postulat lui Einstein, ca o generalizare a principiului mecanic al relativității Galilean tuturor proceselor fizice, susține, în consecință, că legile fizicii sunt invariante în ceea ce privește alegerea inerțial de referință, iar ecuațiile care descriu aceste legi sunt identice în formă în toate sistemele de referință inerțiale. Conform acestui postulat, toate sistemele de referință inerțiale complet egale, adică. E. Phenomena (mecanice, electromagnetice, optice etc.) în toate sistemele de referință inerțiale apar în mod egal. Conform celui de-al doilea postulat al lui Einstein, constanța vitezei luminii este o proprietate fundamentală a naturii, care este constatată ca un fapt experimental.
Teoria specială a relativității a necesitat respingerea noțiunilor obișnuite de spațiu și timp adoptate în mecanica clasică, deoarece acestea contraziceau principiul constanței vitezei luminii. A pierdut înțeles nu numai spațiul absolut, ci și timpul absolut.
Postulatele și teoria lui Einstein bazate pe ele au stabilit o nouă viziune a lumii și a noilor concepte spațio-timp, cum ar fi, de exemplu, relativitatea lungimilor și a intervalelor de timp, relativitatea simultană a evenimentelor.
Conform ideilor mecanicii clasice, masa corpului este constantă. Cu toate acestea, la sfârșitul secolului al XIX-lea, sa stabilit în experimente cu electroni în mișcare rapidă că masa unui corp depinde de viteza mișcării sale și
se mărește cu viteză în creștere conform legii
unde este masa de odihnă a punctului material, adică masa măsurată în acel cadru de referință inerțial, în raport cu care punctul material este în repaus; c este viteza luminii în vid; - masa unui punct din cadrul de referință, față de care se mișcă cu viteza. În consecință, masa aceleiași particule este diferită în diferite cadre de referință inerțiale.
Din principiul relativității lui Einstein, care afirmă invarianța tuturor legilor naturii în tranziția de la un inerțial (invarianța este imutabilitatea, constanța, independența) cadrului de referință la celălalt,
invarianța ecuațiilor legilor fizice cu privire la transformările lui Lorentz.
Legea fundamentală a dinamicii lui Newton: se dovedește a fi, de asemenea, invariantă în ceea ce privește transformările lui Lorentz, dacă derivarea timpului de impuls relativist în el este pe dreapta.
Legea fundamentală a dinamicii relativiste a unui punct material are forma
(2) sau (3), unde (4) este impulsul relativist al punctului material.
Din cauza omogenității spațiului în mecanica relativistă, legea conservării momentului relativist este satisfăcută. Momentul relativist al unui sistem închis este păstrat, adică nu se schimbă odată cu timpul. Adesea ei nu stipulează că iau în considerare un impuls relativist, deoarece, dacă corpurile se mișcă cu viteze apropiate. atunci se poate folosi doar expresia relativistă pentru puls.
Analiza formulelor (1), (4) și (2) arată că la viteze mult mai mici decât viteza luminii, ecuația (2) devine legea fundamentală a mecanicii clasice (). În consecință, condiția pentru aplicabilitatea legilor mecanicii clasice (newtoniene) este condiția. Legile mecanicii clasice sunt obținute ca o consecință a teoriei relativității pentru cazul limitator (tranziția este efectuată oficial când). Astfel, mecanica clasică este mecanica macrobotilor care se mișcă la viteze mici (comparativ cu viteza luminii în vid).
Să găsim energia cinetică a unei particule relativiste (un punct material).
Creșterea energiei cinetice a unui punct material pe o deplasare elementară
este egal cu forța de forță asupra acestei deplasări: sau. (5)
Având în vedere acest lucru. și înlocuind expresia (2) în (5), obținem :.
Conversia acestei expresii la faptul că. și formula (1), vom aduce la expresie (6),
adică, creșterea energiei cinetice a unei particule este proporțională cu creșterea masei sale.
Deoarece energia cinetică a unei particule în repaus este zero, iar masa ei este egală cu masa de odihnă. apoi, prin integrarea (6), obținem (7), sau energia cinetică a particulei relativiste are forma (8).
Expresia (8) la viteze este transformată în clasică: (se extinde într-o serie cu., Este legitim să se neglijeze termenii de a doua ordine a micșorării).
Einstein a rezumat poziția (6), presupunând că aceasta este valabil nu numai pentru energia cinetică a particulei (punct material), ci și pentru energia totală, și anume, orice modificare în masă este însoțită de o schimbare în energia totală a particulelor (punctul material): (9).
Prin urmare, Einstein a ajuns la o dependență universală între energia totală a corpului și masa sa. (10).
Ecuația (10), ca și (9), exprimă legea fundamentală a naturii - legea interrelației (proporționalității) dintre masă și energie. Energia totală a unui sistem este egală cu produsul din masa lui pe pătrat al vitezei luminii în vid. Rețineți că energia totală E nu include energia potențială a corpului în câmpul de forță externă.
Legea (10) poate fi scrisă în formă, luând în considerare expresia (7). din care rezultă că și corpul de odihnă (T = 0) are și energie. numită energie de odihnă. Mecanica clasică nu ține cont de energia de odihnă, considerând că energia unui corp în repaus este zero.
Datorită omogenității timpului în mecanica relativistă, ca și în mecanica clasică, legea conservării energiei este îndeplinită. energia totală a sistemului închis rămâne, adică nu se schimbă odată cu timpul.
Din formulele (10) și (4) găsim raportul relativist între energia totală și impulsul particulei :. .
Revenind la ecuația (10), rețineți încă o dată că are un caracter universal. Este aplicabil tuturor formelor de energie, adică se poate argumenta că energia, indiferent de forma ei, este legată de o masă și, dimpotrivă, cu orice masă este conectată
energie definită (10).
Pentru a caracteriza puterea legăturii și stabilitatea unui sistem de orice particule (de exemplu, nucleul atomic ca sistem de protoni și neutroni), ia în considerare energia de legare. Energia de legare a unui sistem este egală cu munca care trebuie folosită pentru a descompune acest sistem în părțile componente ale acestuia (de exemplu, nucleul atomic pentru protoni și neutroni). Energia de legare a sistemului. unde este masa restului de particule în stare liberă; Este masa restului sistemului constituit din particule.
Legea interrelației (proporționalității) dintre masă și energie este confirmată în mod strălucit de experimentul privind eliberarea energiei pe parcursul reacțiilor nucleare. Este folosit pe scară largă pentru a calcula efectele energiei în reacțiile nucleare și transformările particulelor elementare.
Dipol electric. Efectul unui câmp electric pe un dipol. Câmp electric în dielectrică. Polar și molecule nepolare. Polarizarea dielectricilor. Permeabilitatea dielectrică.
(1) - principiul suprapunerii (impunerii) câmpurilor electrice. conform căruia intensitatea E a câmpului rezultat, creată de sistemul de încărcări, este egală cu suma geometrică a intensităților câmpului create la un anumit punct de către fiecare dintre sarcini separat.
Principiul suprapunerii ne permite să calculam câmpurile electrostatice ale oricărui sistem cu taxă fixă, deoarece, dacă tarifele nu sunt taxe punctuale, atunci ele pot fi întotdeauna reduse la un set de sarcini punctuale.
Principiul suprapunerii este aplicabil pentru calcularea câmpului electrostatic al unui dipol electric. Un dipol electric este un sistem de încărcări cu două puncte de aceeași valoare (+ Q. - Q), care sunt mult mai mici decât distanța față de punctele considerate ale câmpului. Un vector direcționat de-a lungul axei dipol a unei linii drepte care trece prin ambele încărcături) de la sarcina negativă la cea pozitivă și egală cu distanța dintre ele se numește umăr dipol. Vectorul (2) coincide în direcția brațului dipol și este egal cu produsul încărcării pe braț. se numește momentul dipolului electric sau momentul dipolului (Fig.).
Conform principiului suprapunerii (1), forța E a câmpului dipol la un punct arbitrar. unde și sunt intensitățile câmpului create de taxele pozitive și negative, respectiv.
Dielectricul (ca orice substanță) constă din atomi și molecule. Deoarece sarcina pozitivă a tuturor nucleelor moleculei este egală cu sarcina totală a electronilor, molecula ca întreg este neutră din punct de vedere electric. Dacă înlocuim încărcăturile pozitive ale nucleelor moleculelor cu sarcina totală + Q. situat în centrul "gravitației" încărcărilor pozitive, și încărcarea tuturor electronilor - sarcina totală negativă - Q. situată în centru
"Gravitatea" încărcărilor negative, molecula poate fi considerată ca
Dipol electric cu moment electric, definit de formula (2).
Un prim grup de dielectrici (N2. H2 O2. CO2. CH4.) Cuprind o substanță a cărei molecule au o structură simetrică, adică. E. Center „gravitate“ de sarcini pozitive și negative, în absența unui coincidența extern câmp electric, și, prin urmare, momentul de dipol al moleculei p este egal cu zero. Moleculele unor astfel de dielectrice sunt numite nonpolar. Sub acțiunea unui câmp electric extern, sarcinile moleculelor nepolare sunt deplasate în direcții opuse (pozitive în câmp, negative față de câmp) și molecula dobândește un moment dipol.
Al doilea grup de dielectrici (H2O, NH3. SO2. CO.) Cuprind o substanță a cărei molecule au o structură asimetrică, adică. E. Center „gravitate“ sarcinilor pozitive și negative nu coincid. Astfel, în absența unui câmp electric extern, aceste molecule au un moment dipol. Moleculele unor astfel de dielectrice sunt numite polar. În absența unui câmp extern, totuși, momentele dipol ale moleculelor polare datorate mișcării termice sunt orientate aleatoriu în spațiu, iar impulsul rezultat este zero. Dacă un astfel de dielectric este plasat într-un câmp extern, atunci forțele acestui câmp vor avea tendința să rotească dipolii de-a lungul câmpului și va apărea un moment rezultat nonzero.
Al treilea grup de dielectrice (NaCl, KCl, KBr.) Sunt substanțe ale căror molecule au o structură ionică. Cristalele ionice sunt
Spațiale laturi cu o alternanță obișnuită de ioni de semne diferite. În acestea
cristalele, moleculele separate nu pot fi izolate, dar pot fi considerate ca
un sistem de două sublaturi ionice se introduce unul în altul. Când este suprapus
cristal ionic al câmpului electric, apare o anumită deformare a laturii cristaline sau o deplasare relativă a sublaturilor, ceea ce duce la apariția momentelor dipolului.
Astfel, introducerea tuturor celor trei dielectrici grupe într-un câmp electric extern duce la apariția unui cuplu nenul rezultat izolator electric sau, cu alte cuvinte, la polarizarea dielectric. Polarizarea unui dielectric este procesul de orientare a dipolilor sau apariția unor dipoli orientați pe câmp sub influența unui câmp electric.
În consecință, trei tipuri de dielectric se disting prin trei tipuri de polarizare:
e. sau deformare, polarizarea unui dielectric cu nonpolar
molecule, constând în formarea unui moment dipol indus în detrimentul deformării orbitelor electronice;
orientare. sau o polarizare dipol a unui dielectric cu molecule polare, constând în orientarea momentelor dipol existente ale moleculelor pe câmp. Firește, mișcarea termică previne orientarea moleculară completă, dar efectul combinat al ambilor factori (de câmp electric și mișcare termică) are loc orientarea preferențială a momentelor dipol ale moleculelor din domeniu. Această orientare este cu atât mai puternică, cu atât rezistența câmpului electric este mai mare și temperatura este mai mică;
polarizare ionică a dielectrici cu rețeaua cristalină ionic este de a transfera ioni pozitivi sublatice de-a lungul câmpului și negativ - împotriva domeniu, ceea ce duce la apariția momentelor dipol.
Atunci când un dielectric este plasat într-un câmp electrostatic extern, acesta este polarizat,
adică, achiziționează un moment dipol nonzero. unde este momentul dipol al unei molecule. Pentru o descriere cantitativă a polarizării unui dielectric se utilizează polarizarea cantitativă a vectorului. definit ca momentul dipol al unui volum unitar al unui dielectric :. (2)
Din experiență, rezultă că pentru o clasă mare de dielectric polarizare P este dependentă liniar de intensitatea câmpului electromagnetic E. Dacă izotropă dielectric și E nu este prea mare, atunci (3), în care susceptibilitatea dielectrice a materialului caracterizarea proprietăților dielectrice; - dimensiunea fără dimensiuni; în plus, întotdeauna> 0 și pentru majoritatea dielectricilor (solid și lichid) există mai multe unități (deși, de exemplu, pentru alcool, pentru apă = 80).
Pentru a stabili legile cantitative ale câmpului într-un dielectric, introducem un câmp electrostatic omogen exterior (creat de două infinit
paralel cu planuri încărcate opus) o placă de dielectric omogenă, aranjând-o așa cum se arată în Fig.
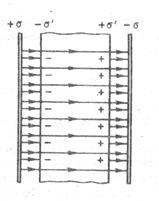
Sub acțiunea câmpului, dielectricul este polarizat, adică se schimbă sarcina: schimbările pozitive de-a lungul câmpului, cele negative se îndreaptă spre câmp. Ca rezultat, în partea dreaptă a dielectricului cu care se confruntă planul negativ, există un exces de sarcină pozitivă cu densitatea de suprafață. în stânga - o sarcină negativă cu o densitate a suprafeței. Aceste sarcini necompensate care apar ca urmare a polarizării dielectricului sunt numite obligatorii. Deoarece densitatea lor suprafață mai mică decât densitatea de purtători liberi de avioane, nu toate câmpul E este compensat cheltuieli dielectrice pe teren: unele dintre liniile de tensiune trec prin izolator, pe de altă parte pauzele privind taxele aferente. În consecință, polarizarea
dielectricul determină o descreștere a câmpului în el în comparație cu originalul
câmp extern. În afara dielectricului.
Astfel, apariția încărcăturilor legate conduce la apariția unui câmp electric suplimentar (un câmp creat prin sarcini legate)
care este îndreptată împotriva câmpului extern (câmpul creat de taxe libere) și îl slăbește. Câmpul rezultat în interiorul dielectricului.
Un câmp (un câmp creat de două avioane infinite încărcate), prin urmare. (4)
Să determinăm densitatea de suprafață a sarcinilor legate. Prin (2). complet
momentul dipolului plăcii dielectrice. unde S este suprafața feței plăcii, d este grosimea ei. Pe de altă parte, momentul dipolului total, conform (3), este egal cu produsul sarcinii legate de fiecare față cu distanța d între ele, adică. Astfel. sau (5), adică densitatea de suprafață a sarcinilor legate este egală cu polarizarea P.
Substituind în (4) expresiile (5) și (3), obținem unde intensitatea câmpului rezultat în interiorul dielectricului este. (6)
Cantitatea dimensională (7) se numește permitivitatea dielectrică a mediului. Comparând (6) și (7), vedem că arată cât de multe ori câmpul este slăbit de un dielectric, caracterizând cantitativ proprietatea unui dielectric de a polariza într-un câmp electric.