Impuls și energie în teoria specială a relativității:
In mecanica-tivistic relativistă legea conservării impulsului: pentru orice proces în care un sistem închis, impulsul său (.. Adică suma geometrică a produselor din masa relativistă a tuturor componentelor sistemului în viteza lor) nu sa schimbat etsya. Ecuația de bază a dinamicii relativiste are forma
- puls de corp (punct material) în mehanike.Mozhno relativiste arată că ecuația (7.21) satisface Lorentz invarianță, dacă trecerea de la un sistem de referință inerțial pentru a converti celelalte componente de forță de-a lungul axelor definite de lege. La viteze reduse (<<с) масса те-ла mm0 =const и релятивистское уравне-ние (7.21) совпадает с основным законом ньютоновской динамики (2.5), а импульс тела является линейной функцией его скорости: p=m0 v=mv. У всех тел масса покоя m0>0. Prin urmare, așa cum se arată în formulele (7.20) și (7.22), masa relativistă și impuls trebuie să crească la infinit tinde viteza de corp la viteza luminii în vid. Toate forțele reale sunt finite în magnitudine, iar efectul lor asupra corpului este limitat în timp. Nu pot imprima un trup infinit de mare impuls. În consecință, viteza corpului față de orice cadru de referință inerțial nu poate fi egală cu viteza luminii într-un vid, dar întotdeauna mai mică decât aceea. Această afirmație este valabilă și pentru atomi, molecule și toate particulele elementare, cu excepția fotonilor. Să găsim expresia energiei cinetice a unui punct material în mecanica relativistă. Incrementul energiei cinetice a unui punct material în deplasarea elementară dr dl muncă egală Sauveur-a fi rezolvată la această forță în mișcare a F, care acționează asupra unui punct material:
unde v este viteza unui punct. Atunci când viteza unui punct material se schimbă, creșterile energiei sale cinetice și masa relativistă sunt proporționale unul cu celălalt:
Energia cinetică a punctului staționar ( = 0) este zero, iar masa relativistă este m0. Prin urmare, integrarea (7.24) în raport cu m de la m0 la m, obținem următoarea expresie pentru energia cinetică a unui punct material:
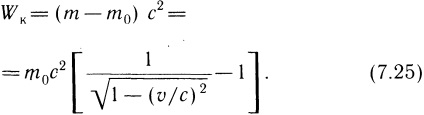
Folosim extinderea seriei Taylor:
E
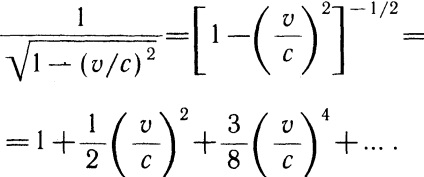
Astfel, la viteze mici mișcarea particulelor din energia cinetică calculată din formula relativistic XYZ (7.25) coincide cu valoarea acestui-em energie în mecanica newtoniană. Cu toate acestea, la viteze mari imagini clorhidric puncte din energia cinetică Wc = (m-m0) 2 și se deosebește de m0 2/2, și de la m0 2/2. Formulele (7.24) și (7.25) se aplică, de asemenea, unui sistem de puncte materiale (de exemplu, un corp rigid) care se deplasează ca o singură unitate cu o viteză v.