1. Tensiuni normale în tensiune și compresie
2. Determinarea deformării longitudinale și transversale. Legea lui Hooke
3. Probleme statice nedeterminate
4. Tensiuni de temperatură
5. Tensiuni de montare
1. Forțe normale de întindere și compresiune
Dacă suprafața caroiajul tija prismatice aplicate paralel și perpendicular pe axa tijei, și să exercite o forță de tracțiune la acesta, este posibil să se asigure că linia grilă și după deformare rămân reciproc perpendiculare (vezi. Fig. 1).
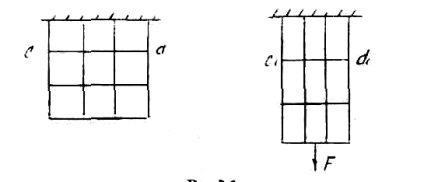
Toate liniile orizontale, de exemplu, cd, se vor deplasa în jos, rămânând orizontale și drepte. De asemenea, putem presupune că în interiorul tijei va exista aceeași imagine, adică "secțiunile transversale ale tijei, plane și normale față de axa lor înainte de deformare, rămân plane și normale față de axă și după deformare". Această ipoteză importantă se numește ipoteza secțiunilor plane sau ipoteza Bernoulli. Formulele obținute pe baza acestei ipoteze sunt confirmate de rezultatele experimentelor.
O astfel de imagine a deformării dă motive să creadă că doar tensiuni normale, care sunt aceleași în toate punctele secțiunii, acționează în secțiunile transversale, iar tensiunile tangențiale sunt zero. Dacă au existat tensiuni de forfecare, atunci ar exista o deformare unghiulară, iar unghiurile dintre liniile longitudinale și transversale ar înceta să fie drepte. Dacă tensiunile normale nu erau identice în toate punctele secțiunii, unde tensiunile erau mai mari, ar exista mai multe deformări și, prin urmare, secțiunile transversale nu ar fi plane și paralele. Având în vedere ipoteza secțiunilor plane, stabilim acest lucru.
Deoarece forța longitudinală este rezultatul forțelor interne
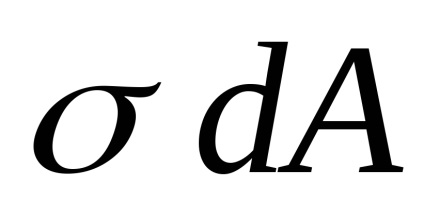
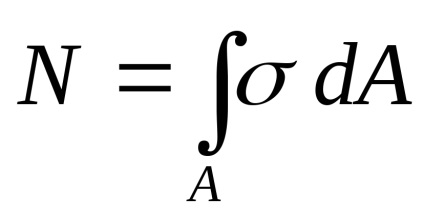
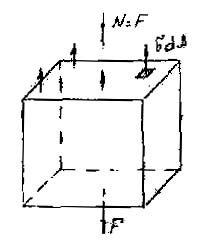
Constantele pot fi scoase din semnul integral:
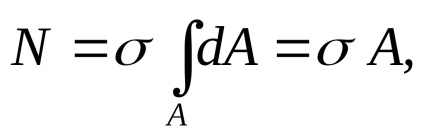
unde A este aria secțiunii transversale.
Obținem o formulă pentru găsirea tensiunilor normale sub tensiune sau compresiune:
Aceasta este una dintre cele mai importante formule din rezistența materialelor, așa că o vom identifica în cadru și vom acționa și în viitor.
Când se întinde

Dacă numai o forță exterioară F acționează asupra fasciculului, atunci
iar tensiunea poate fi determinată de formula:
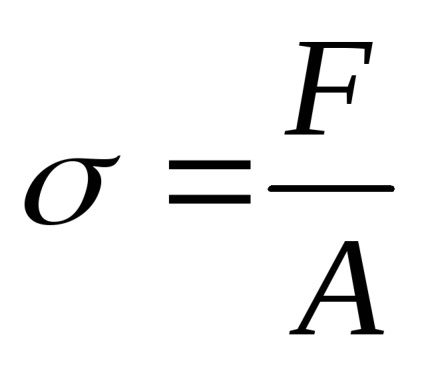
2. Determinarea deformării longitudinale și transversale
În stadiul elastic al funcționării majorității materialelor structurale, tensiunile și deformările sunt legate de o dependență directă, numită legea lui Hooke:
unde E este modulul de elasticitate longitudinal sau modulul lui Young, măsurat în MPa, caracterizează rigiditatea materialului, adică abilitatea de a rezista deformărilor, valorile sale sunt date în tabelele din manual;


l lungimea inițială, m.
Cu cât este mai mare valoarea modulului de elasticitate longitudinală E, cu atât este mai mică deformarea. De exemplu, pentru oțel E = 2,110 5 MPa, și pentru fontă E = (0,75 ... 1,6) 10 5 MPa, astfel încât proiectarea elementului de fier primește o deformare mare în condiții identice, altele decât cele cu oțel. Aici nu ar trebui să fii confundat cu faptul că tija din oțel va avea o deformare mult mai mare decât fonta. Nu este vorba despre limitarea tensiunii, ci despre deformarea în etapa elastică, adică fără apariția deformărilor plastice și cu aceeași încărcătură.
Transformăm legea lui Hooke, înlocuind din ecuația (3.3):
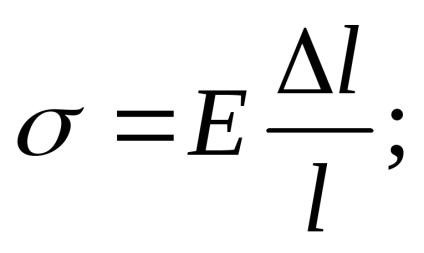
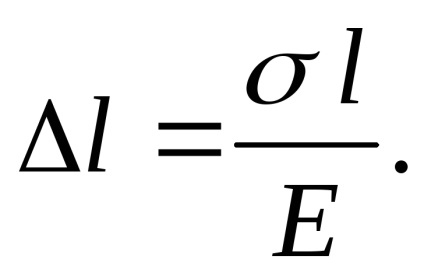
Noi substituim valoarea

Am obținut o formulă pentru alungirea (scurtarea) absolută a tijei. Când se întinde

Când este întins, tija devine mai subțire, iar compresia - mai groasă. Schimbarea dimensiunilor secțiunii transversale se numește deformare transversală. De exemplu, pentru o secțiune dreptunghiulară, înainte de încărcare, au fost lățimea b și o înălțime a secțiunii h. și după încărcare - b1 și h1. Deformarea laterală relativă pentru lățimea secțiunii:
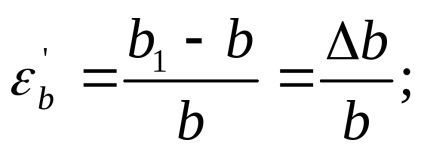
pentru înălțimea secțiunii:
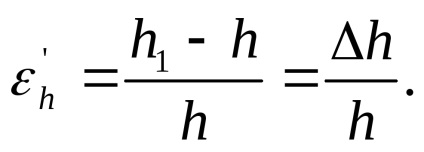
În materiale izotropice, proprietățile sunt identice în toate direcțiile. Prin urmare:
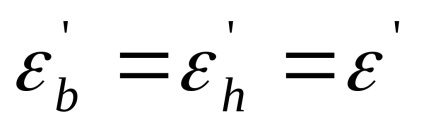
La întindere, deformarea transversală este negativă și sub compresie, este pozitivă.
Raportul dintre efortul transversal și cel longitudinal se numește coeficientul de deformare transversală sau raportul Poisson:
Sa stabilit experimental că în etapa elastică de funcționare a oricărui material valoarea
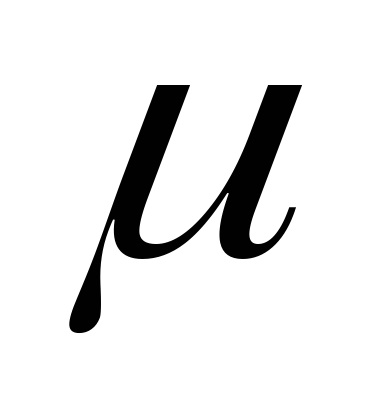
Din dependență (5) este posibil să se primească următoarea formulă:
Când se întinde (comprimarea) secțiunile transversale ale barei se deplasează în direcția longitudinală. Mișcarea este o consecință a deformării, însă aceste două concepte trebuie să fie clar delimitate. Pentru tija (vezi figura 3), determinăm amploarea deformării și construim diagrama de deplasare.
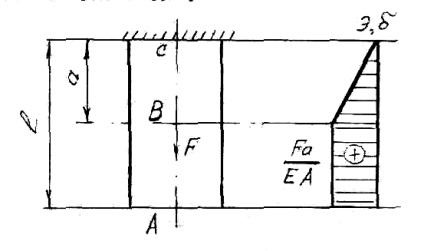
Așa cum se poate vedea din desen, segmentul tijei AB nu se întinde, ci se va mișca, deoarece segmentul CB va fi extins. Elongația sa este:
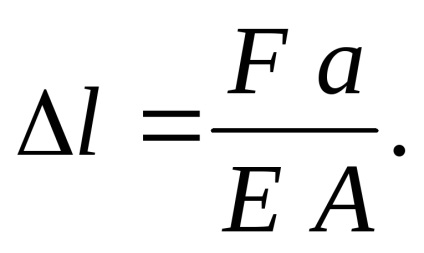
Indicăm deplasările secțiunilor transversale prin



3. Probleme statice nedeterminate
Static nedeterminat este considerat a fi sisteme ale căror eforturi nu pot fi determinate cu ajutorul doar a ecuațiilor de statică. Toate sistemele statice indeterminate au conexiuni "extra" sub formă de elemente de fixare suplimentare, tije și alte elemente. Legăturile "superficiale" sunt numite deoarece nu sunt necesare din punctul de vedere al asigurării echilibrului sistemului sau al imutabilității geometrice, iar dispozitivul lor urmărește obiective constructive sau operaționale.
Diferența dintre numărul de necunoscute și numărul de ecuații de echilibru independente care pot fi făcute pentru un anumit sistem caracterizează numărul de necunoscute necunoscute sau gradul de indeterminare statică.
Sistemele statice nedeterminate sunt rezolvate prin construirea ecuațiilor de deplasare a anumitor puncte, numărul cărora trebuie să fie egal cu gradul de indeterminare a sistemului.
Lăsați forța F (Figura 4) să acționeze asupra tijei rigid fixate de ambele capete. Definiți reacția suporturilor.
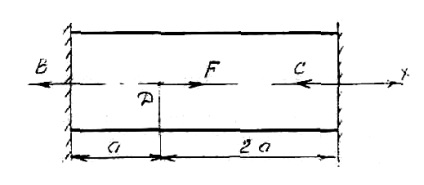
Reacțiile suporturilor sunt îndreptate spre stânga, deoarece forța F acționează spre dreapta. Deoarece greutatea forței acționează de-a lungul unei linii, este posibil să se compună o singură ecuație de echilibru static:
Deci, două reacții necunoscute ale suporturilor B și C și o ecuație de echilibru static. Sistemul este o dată static nedeterminat. Prin urmare, pentru a rezolva aceasta, trebuie să facem o ecuație suplimentară, bazată pe deplasările punctului C. Mentally, vom renunța la sprijinul potrivit. Din forța F, partea stângă a tijei HP va fi întinsă, iar secțiunea C se va deplasa spre dreapta cu valoarea acestei deformări:
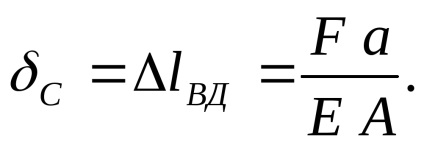
Din reacția suportului C, tija va fi comprimată și secțiunea transversală se va deplasa spre stânga cu cantitatea de deformare a întregii bare:
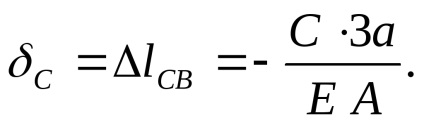
Suportul nu permite ca secțiunea C să se deplaseze nici spre stânga, nici spre dreapta, astfel încât suma deplasărilor de la forțele F și C trebuie să fie egală cu zero:
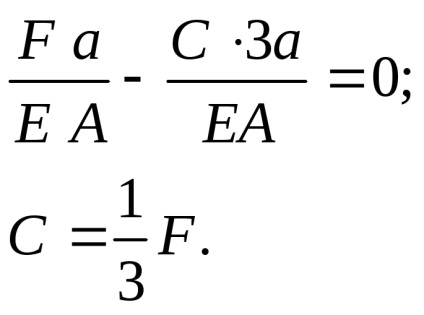
Substituind valoarea lui C în ecuația echilibrului static, definim a doua reacție a suportului:
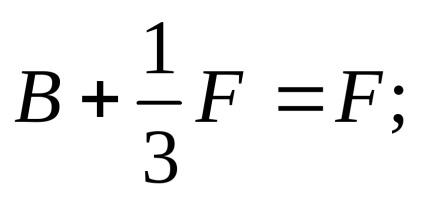
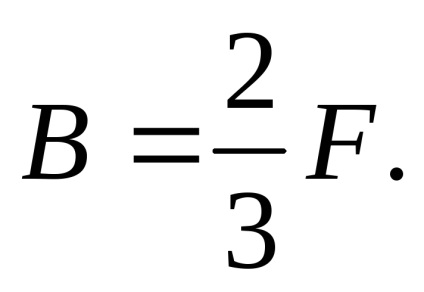
4. Tensiuni de temperatură
Sistemele statice nedeterminate pot genera solicitări atunci când temperatura se schimbă. Lăsați bara, închisă rigid din ambele capete, să fie încălzită la o temperatură

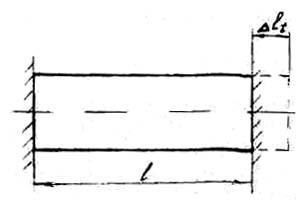
Când sunt încălzite, corpurile se extind, iar tija va avea tendința de a se alungi cu cantitatea:
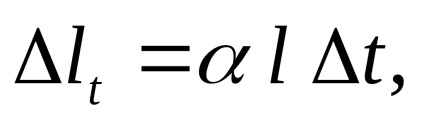
unde

l - lungimea inițială.
Suporturile nu permit ca tija să se extindă, astfel încât tija este comprimată de cantitatea:
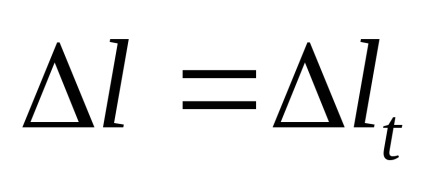
Conform formulei (4):
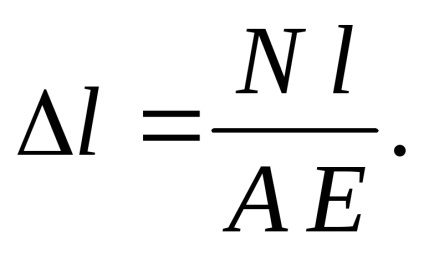
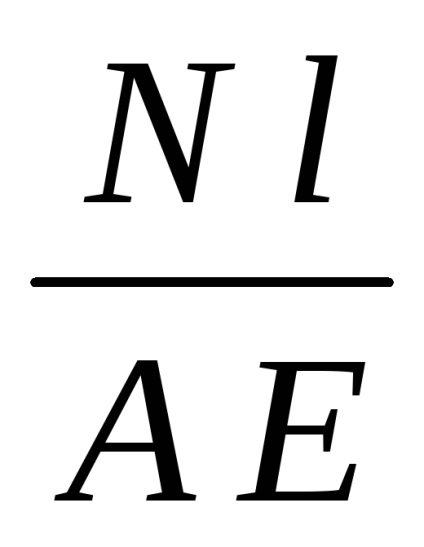
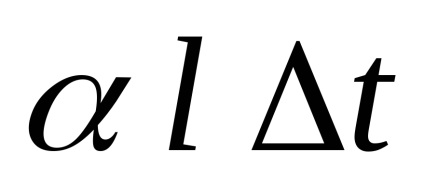
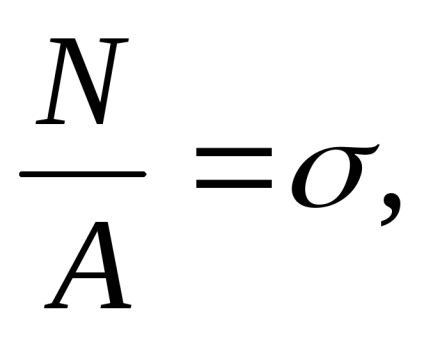
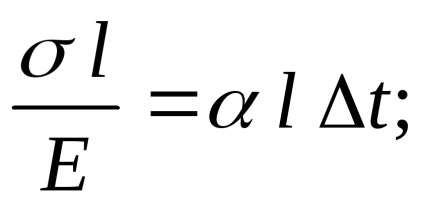
După cum se vede din formula (7), tensiunile termice sunt independente de lungimea tijei și depinde numai de coeficientul de dilatare liniară, modulul de elasticitate se schimbă și temperatură longitudinale.
Temperaturile pot atinge valori ridicate. Pentru a reduce designul lor oferă o lacune speciale de temperatură (de exemplu, lacune în îmbinările șinelor) sau dispozitivul de compensare (de exemplu, coturi în țevile).
5. Tensiuni de montare
Elementele structurii pot avea abateri în dimensiune în timpul fabricării (de exemplu, datorită sudării). La asamblare, dimensiunile nu se potrivesc (de exemplu, găurile de șuruburi) și se depun eforturi pentru asamblarea ansamblurilor. Ca urmare, forțele interne apar în elementele structurale fără a aplica o sarcină externă.
Lăsați o tijă să fie introdusă între două garnituri rigide, lungimea căreia cu o cantitate a este mai mare decât distanța dintre suporturi (a se vedea figura 6). Tija va avea compresie. Definim eforturile folosind formula (4):
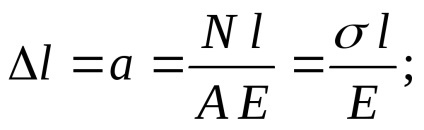

Așa cum se poate observa din formula (8), tensiunile de montare sunt direct proporționale cu eroarea în dimensiunile a. Prin urmare, este de dorit să aibă a = 0. în special pentru tije de lungime mică, deoarece

Cu toate acestea, în sistemele statice indeterminate, tensiunile de montare sunt folosite special pentru a mări capacitatea de încărcare a structurii.