Numărul de fringe de interferență (din banda zero) este un număr polinomial. Pentru banda cu numărul m, diferența de traiectorie a undelor interferante este mlim.
Dacă frecvența de zgomot de lumină, zgomot și lungimea de undă și numărul de lungimi de undă, care este plasat pe diferența cale optică la un punct fix de pe ecran, și ordinea de interferență m.
Dacă ordinul de interferență este zgomotos de unul (m = 1), atunci numărul de fringe interferență pentru punctul de ecran selectat este, de asemenea, zgomotos de unul. Aceasta corespunde unei deplasări de zgomot a modelului de interferență pe o distanță egală cu lățimea benzii. Cu această mișcare, modelul de interferență este complet "murdar". Să vedem acum ce schimbare a frecvenței și lungimii de undă a luminii corespunde unei modificări în ordinea interferenței pe unitate.
Regiunea de vizibilitate ridicată a modelului de interferență cu o sursă de lumină cvasi-monocromatică
La limita regiunii "neecranate" a modelului de interferență, ordinul de interferență m zgomot pe unitate (dm = 1). Produsul este egal cu diferența de cale și, prin urmare, nu produce zgomot. Apoi, m (m) = 0. Prin urmare, m λ λ + ⎟ μ ⎞ ⎠ ⎞ ⎜ ⎝ ⎛ ⎞ ⎜ ⎝ ⎠ ⎞ ⎜ ⎝ ⎛ =
În mod similar, condiția = c / n = const implică
Din egalitatea m / m = / = / cu o menta pentru m = 1, obținem două condiții limită noi pentru regiunea "neecranată" a modelului de interferență:
Dacă luăm acum în considerare faptul că ordinea interferenței este diferența de cale, exprimată în lungimi de undă (m = / ), atunci diferența de traiectorie
=,
Definește granița zonei ecranului în care sunt clar delimitate marginile de interferență.
Mai mult, pentru a rezolva o problemă particulară, este necesar să găsiți o zonă pe ecran în care diferența de drum să nu depășească o valoare dată 2 / . Această problemă este fie pur geometrică, fie geometrică. Dacă doriți să găsiți numărul maxim de franje de interferență observate, acesta este fie egal cu ordinul maxim de interferență (m = / = / ), în cazul în care există dungi pe o parte a benzii de la zero, fie - aproximativ de două ori mai multă interferență.
Coerența temporală
Coerența temporală este legată de coerența de-a lungul razei. Coerența este capacitatea de a interveni. Luați în considerare două puncte pe o rază ca două surse secundare de lumină posibile pentru a observa modelul de interferență. În acest caz, se presupune că distanța de la fiecare punct la ecranul mental este aceeași.
O posibilă variantă a schemei optice este prezentată în Fig. 23. Aici, A și B - cele două puncte selectate de-a lungul razei în care a pus mental placa semitransparente pentru a obține un model de interferență pe C. Prin ecran Ipoteza AC = problema BC.
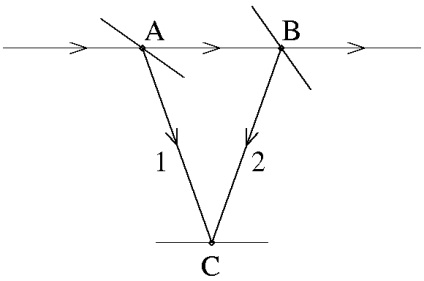
Diferența de cale optică pentru fasciculele de interferență 1 și 2, așa cum se vede din Fig. 23 este egal cu AB. Dacă AB depășește velichinu 2 / , apoi, așa cum sa arătat mai sus, modelul de interferență este „neclară“ și, prin urmare, sursele de lumină secundare la punctele A și B sunt incompatibile. Distanța dintre punctele A și B la care începe să se întâmple este numită lungimea coerenței de-a lungul razei (coerența longitudinală). Îl denumeam ca L ||. atunci
Această formulă este adesea folosită pentru rezolvarea problemelor.
Împreună cu noțiunea de "coerență longitudinală", este folosit conceptul de "coerență temporală", care este aproape de acesta. Faza a câmpului de lumină de la punctul A (vezi. Fig. 23) la momentul t egal cu faza câmpului la punctul B la momentul t + , gde- timp de propagare a luminii de la A la B. Prin urmare, coerența câmpului la punctele A și B într-un singur momentul momentului t este exact același cu coerența la un punct B, dar la două momente diferite t și t + .
Timp , pentru care lumina trece lungimea de coerență L ||. numită coerența timpului. Din expresia binecunoscută pentru viteza luminii c / n = , obținem o relație simplă pentru timpul de coerență:
Se poate vedea coerența câmpului de lumină la punctele A și B într-o oarecare măsură. Lungimea de undă este zgomotoasă. În consecință, numărul de lungimi de undă, care se potrivește segmentului AB, este zgomotos. Diferența de fază este proporțională cu zgomotul de la punctele A și B. Rezultatul interferenței depinde de diferența de fază. Dacă diferența de fază la punctele A și B este mai zgomotoasă decât 2π, atunci câmpul din aceste puncte este incoerent, dacă este mai mic, atunci câmpul este coerent. În această formă, condiția coerenței câmpului la punctele A și B nu necesită localizarea acestor puncte de-a lungul razei sau luarea în considerație a câmpului în ele în același timp.
Subliniem faptul că condiția "zgomote de diferență de fază mai mare de 2" nu trebuie confundată cu condiția "diferența de fază este mai mare de 2".