Prezentare pe tema: "Un dreptunghi este o paralelogramă a cărei unghiuri sunt drepte. BC D Pentru dreptunghiul, proprietățile paralelogramului dreptunghiului sunt îndeplinite." - Transcriere:
1

2 Un dreptunghi este o paralelogramă cu toate unghiurile drepte. Sun D Pentru dreptunghiului sunt efectuate pentru proprietățile dreptunghiului paralelogramului proprietăți executate de paralelogram 0. 1 paralelogram laturile opuse sunt unghiuri egale și opuse sunt diagonalele egale ale paralelogramului bisect punctul de intersecție.
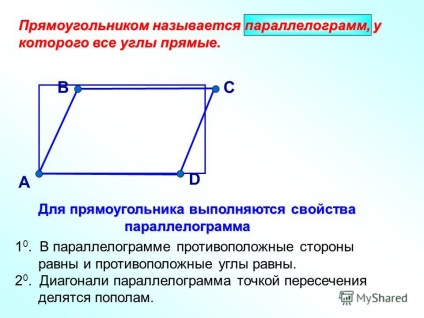
3 Proprietatea specială a dreptunghiului. Diagonalele dreptunghiului sunt egale. A B C D este dată: Dată: ABCD dreptunghi Dovedeste: Dovedeste: AC = VDDokazatelstvo: ACD = DBA la catete Prin urmare, AC = BD. AD - partea comună a AB = CD, ca părți opuse
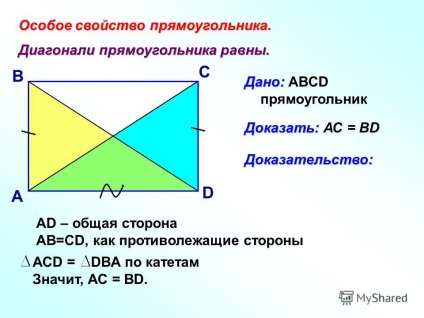
4 Instrucțiunea converse este un semn al unui dreptunghi. Dacă diagonalele sunt egale în paralelogramă, atunci paralelogramul este un dreptunghi. A B C D este dată: Dată: paralelogramul ABCD AC = BD Dovedeste: Dovedeste: ABCD pryamougolnikDokazatelstvo: AD - partea comună AC = BD prin ipoteza AB = CD ca laturile opuse ale paralelogramului ACD = DBA trei laturi Prin urmare, A = D. Cantitatea unghiuri ale patrulaterului 360 0, aceasta înseamnă că toate unghiurile sunt egale cu 90 0 Apoi, C = a și D = B
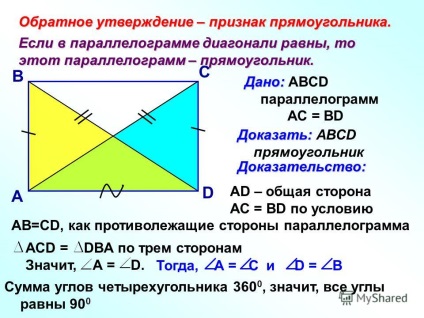
5 Dovada ca paralelajul ABCD este un dreptunghi A C B D D
6 dreptunghi ABCD efectuat bisector A care se intersectează BC lateral la punctul M, VM. MS = 2. 3. Localizați soarele, dacă ABCD perimetru este de 56 cm B A D C 3 F F = 56cm = 56cm 2 (2 + 2 + 3) = 56 r = 28cm = 28cm p 2x + 2x + 3x = 2 28 + 2 + 3 = 28 M × 2 ×
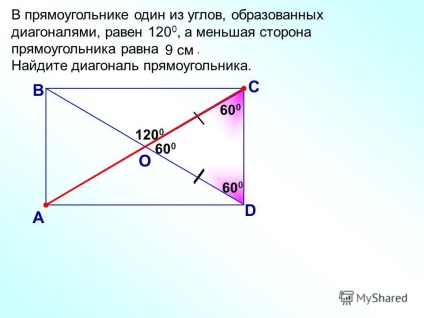
7 60 0 În dreptunghi, unul dintre unghiurile formate de diagonale este 120 0, iar partea mai mică a dreptunghiului este de 9 cm. Găsiți diagonala dreptunghiului B A C D O cm
8 Găsiți unghiul ascuțit între diagonalele dreptunghiului dacă unul dintre ele împarte unghiul la vârful dreptunghiului față de 2. 7. M C P T O. 2x 7x
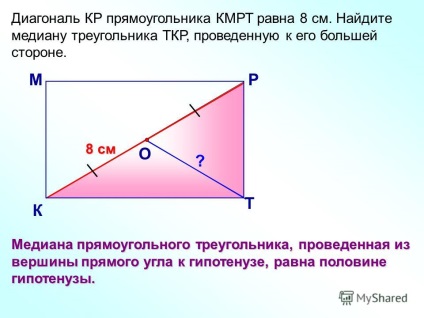
Despre 9 Diagonal KR KMRT dreptunghi este de 8 cm. Gaseste mediana triunghiului TCR realizat de partea sa mai mare. M C R T 8 cm Mediana unui triunghi în unghi drept, trasată de la vârful unghiului drept la hypotenuse, este jumătate din hipotensiune.
10 Un romb este un paralelogram în care toate laturile sunt egale. O romburi efectuată pentru proprietățile proprietăților paralelogram sunt efectuate pentru paralelogram romburi 0. 1 paralelogram laturile opuse sunt unghiuri egale și opuse sunt diagonalele egale ale paralelogramului bisect punctul de intersecție. ВС D
11 Proprietatea specială a diamantului. diagonalele romb perpendiculare între ele și împartă colțuri jumătate este dat: Având în vedere: ABCD romburi A B C D Dovedeste: Dovedeste: AC BD BAC = DACDokazatelstvo: Despre AB = AD prin definiție romburi AVD p / b Apoi, AO - mediana Deoarece diamant - paralelogram , apoi BO = DO. BAC = DAC ca VDAO - altitudine AO - bisector
12 408. Atributul unui romb Un semn al unui romb. Dacă diagonalelor paralelogramului sunt perpendiculare, paralelogramul este un romb A B C D Dovedeste: Dovedeste: ABCD rombDokazatelstvo: Date fiind: Date fiind: paralelogramul ABCD AC BD On ABO = CBO = SDO = DAO Prin cateta AB = BC = CD = DA ABCD romburi prin definiție
13 Dovada că paralelogram ABCD - romb A C B D D / /
14 408. Atributul unui romb Un semn al unui romb. Dacă diagonala paralelogramului este bisectoarea unghiului său, paralelogramul este un romb A B C D Dovedeste: Dovedeste: ABCD rombDokazatelstvo: Dată: Dată: ABCD paralelogram AC - bisector Va d = 2 = 43 = Justify ABC p / w AD = BC, adică. a. Paralelogram ABCD BC = BA; АВС р / б АВ = DC, deoarece. ABCD paralelogram ABCD diamant prin definiție
15 Găsiți perimetrul diamantului. A B C D 5 m 60 0 Exerciții planimetrice în desenele finite
16 Găsiți perimetrul diamantului. EA = 1 m A V C D 1m1m1m1m E F Exerciții planimetrice în desenele finite
17. 35 0. 55 0. 70 0. Găsiți toate unghiurile necunoscute. A B C D 20 0 S Exerciții planimetrice în desene finale
18 3,5 cm Unul dintre colțurile diamantului este de 150 de grade și înălțimea lui este de 3,5 cm. Găsiți perimetrul diamantului. A B C D S
19 433. Perpendiculele VC și VM pe laturile AD și DC sunt extrase din vârful B al diamantului ABCD. Dovedeste ca raza BD este bisectorul unghiului CME. IN A C D K M
20 Latura diamantului este egală cu una dintre diagonalele sale. Care este magnitudinea unghiului mai mare al acestui diamant. A B C D 60 0
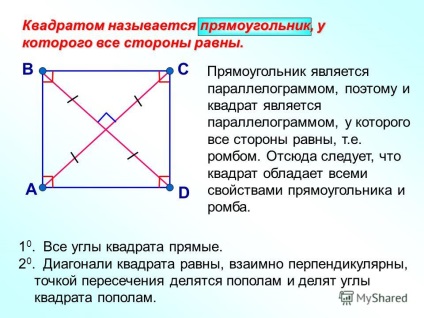
21 Un pătrat este un dreptunghi cu toate laturile egale. A 1 0. colțuri Toate pătrate drepte diagonala unui pătrat sunt egale, reciproc perpendiculare, punctul de intersecție sunt împărțite în jumătate și se împarte colțurile pătrat în jumătate. BC D Un dreptunghi este un paralelogram, astfel încât pătratul este, de asemenea, un paralelogram în care toate laturile sunt egale, adică romburi. Rezultă că pătratul are toate proprietățile unui dreptunghi și unui romb.
22 Găsiți perimetrul pătratului. А ВС D 6мм Е mm Exerciții pe planimetrie pe desene gata
23. 95 0. 45 0. Găsiți toate unghiurile necunoscute ale pătratului. А ВС DE F. 85 0. 45 0 O Exerciții planimetrice în desenele finite
24 punctul M este situat în zona interioară a unui ABCD pătrat, astfel încât distanța de la ea la laturile AB, BC și CD-uri, respectiv, sunt proporționale cu numerele 2, 5 și 7, iar distanța de la M la linia AD este de 4 m. Găsiți perimetrul unui pătrat. În A C D M P -. 2x7x 5x 4m