Prezentare pe tema: "Să se familiarizeze cu definiția unghiurilor adiacente, cu teorema privind unghiurile adiacente și dovada ei, cu consecințe din teorema asupra unghiurilor adiacente, cu tipuri de unghiuri". - Transcriere:
1

2 Să cunoaștem definiția unghiurilor adiacente, cu teorema privind unghiurile adiacente și dovada ei, cu consecințele teoremei asupra unghiurilor adiacente, cu tipuri de unghiuri. Aflați cum să rezolvați problemele legate de acest subiect.

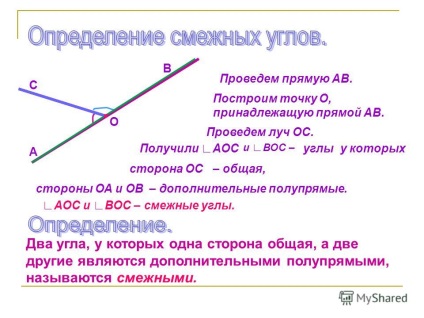
3 Desenați linia AB. Construim un punct 0 aparținând liniei AB. Trageți fasciculul sistemului de operare. Obținută partea AOS din partea OS OA și AOS AOS și BOC - unghiurile adiacente. A B C O și BOC - unghiurile în care - totalul, - jumătățile suplimentare. Două unghiuri în care o parte este obișnuită și celelalte două sunt semilini complementare se spune că sunt adiacente.
4 Suma unghiurilor adiacente este de 180 °. și în c Dano: (a) și (toate) sunt adiacente Prove: (a) + (vs) = 180 ° Proof. (av) - desfășurată, înseamnă (ave) = 180 ° (măsurați unghiurile) Radiația c trece între laturi (av), apoi (av) = (ac) + (vs), (sv în măsurarea unghiurilor). Sa constatat că (ac) + (soare) = 180 °.

5 1. Dacă două unghiuri sunt egale, atunci unghiurile adiacente acestora sunt egale cu 2; 3 și 4 sunt adiacente, 1 = 3, atunci este evident că 2 = 4. Dacă
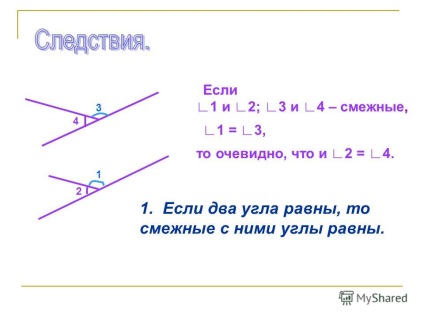
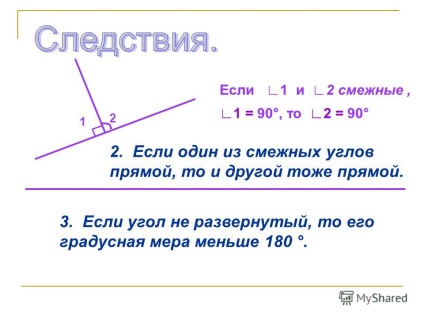
6 Dacă 1 și 2 sunt adiacente, 1 = 90 °, apoi 2 = 90 °. Dacă unul dintre unghiurile adiacente este drept, atunci celălalt este de asemenea o linie dreaptă. 3. Dacă unghiul nu este extins, atunci măsura gradului său este mai mică de 180 °.
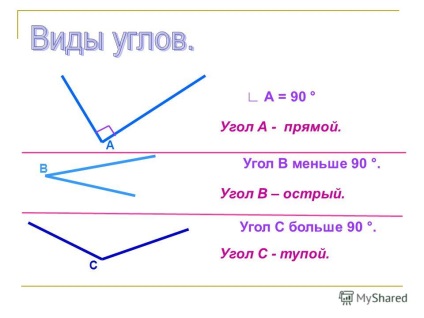
7 A = 90 ° Unghiul A este o linie dreaptă. Unghiul B este mai mic de 90 °. În colțul B - ascuțit. Unghiul C este mai mare de 90 °. C Unghiul C - prost.
8 Găsiți unghiuri adiacente dacă unul dintre ele este de 4 ori mai mic decât celălalt. 1 2 Având în vedere: 1 și 2 adiacente 1 este de 4 ori mai mică decât 2. Găsiți: 1 și 2. Soluție. Fie i = x °, apoi z = (4x) ° = 180 °, (prin teorema pe unghiuri adiacente). Să facem ecuația: x + 4x = 180 5x = 180 x = 36 1 = 36 ° 1) 2 = 36 4 = 144 ° Răspuns: 36 °, 144 °
1. 1. Cunoaște teorema privind unghiurile adiacente, dovezile și corolarul din teoremă, (subsecțiunea 14) 2. 2 (verbal), 4 (1, 2, 4), p. Estimări lecții:
10