În ciuda simplității funcției logice realizate, nu există multe moduri de a crea invertoare (vezi Figura 2.2).
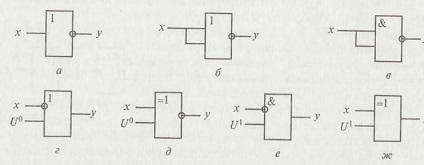
Fig. 2.2. Scheme de implementare a inversării pe diverse elemente: a - invertor; b - OR-NU; in-AND-NOT; g - implicatorul; q - echivalență; e - interdicție; g - exclusiv OR
Invertorul în sine și elementele OR-NOT și NAND nu necesită tensiuni de referință suplimentare. Implicatorul și elementul de echivalență au nevoie de un nivel logic zero, iar elementele interzicerii și OR exclusive se află în nivelul de unitate.
Modalitățile de implementare a disjuncției (figura 2.3) sunt semnificativ mai mici decât cele considerate anterior pentru substituții.
Rețineți că este mai ușor să înlocuiți separatoarele cu elemente OR-NON și implicatoare, care includ o operație de disjuncție ca una dintre cele mai importante. În acest caz, doar două elemente sunt necesare pentru înlocuire (Figura 2.3b). În cazul utilizării elementelor NAND și interzicerea înlocuirii unui întrerupător, este necesar să existe trei elemente (Figura 2.3 d).
Compoziția și structura schematică a conjunctorilor (Figura 2.4) sunt similare cu schemele prezentate în Fig. 2.3, numai aici operația de disjuncție este înlocuită de o conjuncție și invers.
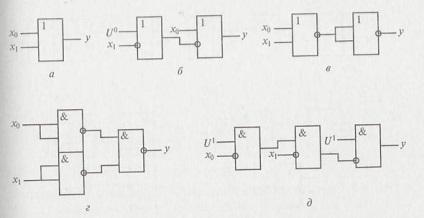
Fig. 2.3. Diagrame de implementare a disjuncției pe diverse elemente: a - întrerupător; b - implicatori; in - OR-NOT; g - AND-N; d - interdicție
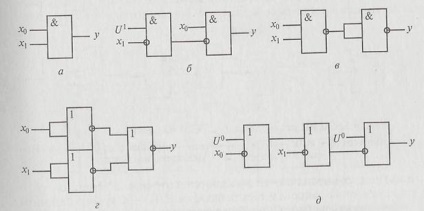
Fig. 2.4. Scheme de realizare a conjuncției pe diverse elemente: a - conjunctor; b - interdicție; in-AND-NOT; g - OR-NU; d - implicatori
Pentru implicatori, opțiunile de înlocuire sunt chiar mai mici (Fig.2.5) decât pentru conjunctori. Este de remarcat că chiar și operația de disjuncție din elementul OR-NOR "nu ajută", deoarece acestea sunt necesare în numărul de trei bucăți.
În circuitele TTL, elementele logice complexe AND-OR și AND-OR-NOT sunt foarte des folosite, ceea ce permite implementarea unor funcții logice reprezentate în forme normale disjunctive directe și (sau) inverse. Cel prezentat în Fig. 2.6 și elementul logic 2-4-2-3I - 4 sau - NU este capabil să efectueze următoarea operație logică:
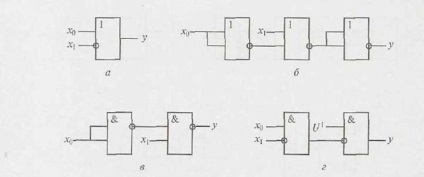
Fig. 2.5. Scheme de implementare a implicațiilor asupra diferitelor elemente: a - implicator; b - OR-NU; in-AND-NOT; d - interdicție
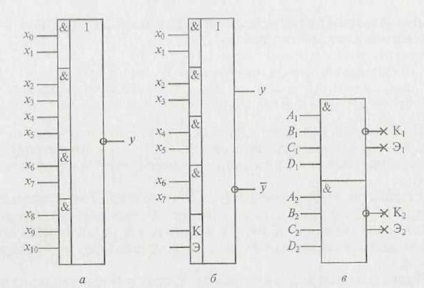
Fig. 2.6. Variante ale elementelor logice AND-OR și I-OR-NOT: a - 2-4-2-3I - 4 sau - NU; b - 2-2-2-2И - 4ИЛИ / 2-2-2-2И - 4ИЛИ-НЕ cu posibilitatea extinderii prin OR; - două extensie logică cu patru intrări pe OR
In alte cipuri, care sunt combinate elemente nu sunt folosite doar pentru sau agenți de diluare, ci conduce și ieșirile inverse simultan (fig. 2.6 b). Chips, care sunt extensoare sau (fig. 2.6), au colector suplimentar outs (C) și emițător (E) conectate la bornele respective ale elementului principal AND-OR / AND-OR-NOT (vezi. Fig. 2.6 b).
Cele prezentate în Fig. Opțiunile de 2,6 nu epuizează lista elementelor logice AND-OR și I-OR-NOT, produse de industrie. Soiurile lor sunt enumerate în cărțile de referință corespunzătoare.
Elementele luate în considerare ne permit să obținem dispozitive de complexitate diferite și să realizăm funcții reprezentate în formă disjunctivă normală sau inversată, care este în concordanță cu funcționarea minimizării cu privire la zerouri.
Aceste elemente au fost utilizate pe scară largă cu microcircuite integrate simple: invertoare, elemente de NAND și altele.
De exemplu, luați în considerare implementarea funcțiilor de echivalență și inegalitate bazate pe elementele și invertoarele AND-OR-NE (figura 2.7). Logica construirii acestor scheme rezultă din inversul reciproc al funcțiilor de echivalență și non-egalitate.
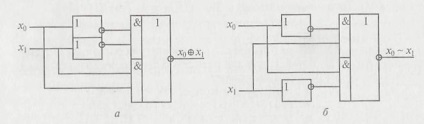
Fig. 2.7. Schemele de dispozitive cu excepția OR (a) și a echivalenței (b) pe baza invertoarelor și a elementelor AND-OR-HE
De asemenea, este interesantă implementarea funcției de echivalență cu utilizarea elementului NAND (Figura 2.8).
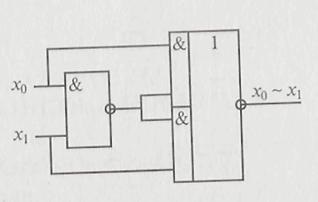
Fig. 2.8. Equivalence circuit device bazat pe elemente NAND și AND-OR-NOT
Motivul pentru această schemă rezultă din transformările formulei de echivalență de bază cu ajutorul formulelor lui Morgan