Zona, proiect de internet

În acest articol, vom afla cum se calculează suprafața figurii.

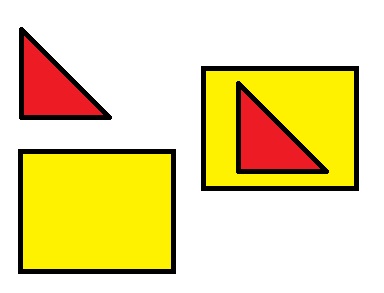
Compara zona de diferite forme poate fi un mod de a impune. Uită-te la imagine. Vedem două figuri: un triunghi și un dreptunghi. Pentru a le compara, putem impune o cifră mai mică pe una mai mare. Triunghiul se potrivește complet în dreptunghi, ceea ce înseamnă că triunghiul este mai mic decât dreptunghiul.

Dar nu este întotdeauna posibilă compararea ariei figurilor în acest fel. Apoi, puteți împărți cifra în pătrate egale și numărați numărul de pătrate care intră în această cifră.

Figura arată două cifre. Prin suprapunerea acestor cifre este imposibil de comparat. Am rupt aceste figuri în pătrate cu aceeași zonă. Acum puteți calcula numărul de pătrate care intră în aceste cifre. Prima cifră se potrivește cu 6 pătrate, iar cea de-a doua 8. Aceasta înseamnă că zona primei figuri este mai mică decât a celui de-al doilea.

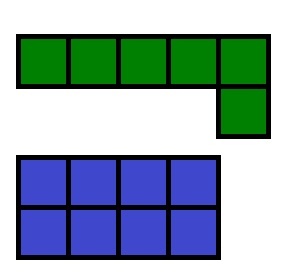
Zona cifrei este egală cu numărul de pătrate unice care compun această cifră.

Dacă pătratul laturii este de 1 cm, atunci suprafața acestui pătrat este de 1 centimetru pătrat (cm 2).

Pătratul pătratului a cărui latură este egală cu 1 decimetru este egală cu 1 decimetru pătrat (dm 2) sau 100 centimetri centimetri (cm 2).

Zona cifrei este notată cu litera latină de capital S.

Să presupunem că trebuie să găsim zona dreptunghiului a cărui lungime este de 6 și 4 cm. Împărțiți dreptunghiul cu centimetri pătrați și calculați suprafața sa.

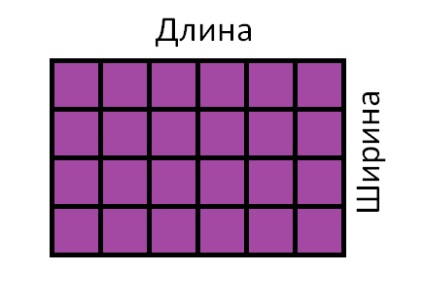
Deci, multiplicați lungimea dreptunghiului cu lățimea sa și obțineți suprafața:

S = 6 × 4 = 24 cm2

Pentru a calcula aria unui dreptunghi. Este necesar să se măsoare lungimea și lățimea în aceleași unități de măsură și să se găsească produsul lor.

Dacă este cunoscută aria dreptunghiului și a lățimii, atunci este ușor de găsit lungimea, trebuie să împărțim zona cu o anumită lungime.

De exemplu, zona dreptunghiului este de 15 cm 2. Lungimea dreptunghiului este de 5 cm. Găsiți lățimea lui:

Dacă figura este complexă, de exemplu, cum ar fi în figură, atunci calculați suprafața acesteia împărțind forma în dreptunghiuri, calculați suprafața lor și adăugați apoi suprafețele rezultate.

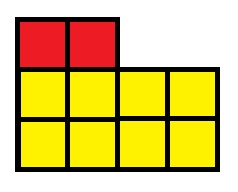
Deci, figura noastră se poate rupe în două dreptunghiuri: prima zonă de 2 cm 2 și a doua arie de 8 cm 2:

S = 2 × 1 + 4 × 2 = 10 cm2

Și cum să găsiți zona unui triunghi cu unghi drept. Pentru a face acest lucru, trebuie să completați triunghiul dreptunghiului, așa cum se arată în figură.

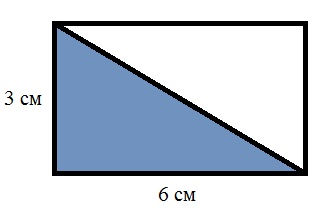
Acum găsiți zona dreptunghiului rezultat și împărțiți-l în jumătate:

S = (3 × 6) ÷ 2 = 9 cm2

Se pare ușor când triunghiul este dreptunghiular. Dacă triunghiul nu are un unghi drept, atunci suprafața sa poate fi calculată după cum urmează:

În figura următoare, vedem un triunghi, a cărui zonă trebuie să o calcurăm, este evidențiată în galben. Vom introduce într-un dreptunghi, așa cum se arată în figură. Lungimea dreptunghiului rezultat este de 5 cm, lățimea este de 4 cm. Vârful triunghiului împarte lungimea dreptunghiului în părți în 3 și 2 cm.

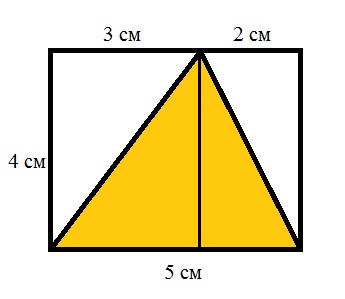
Acum, pentru a găsi zona triunghiului nostru, trebuie să calculam suprafața celor două triunghiuri rectangulare obținute și să le adăugăm:

S1 = (3x4) ÷ 2 = 6 cm2

S2 = (2 × 4) ÷ 2 = 4 cm2

S = S1 + S2 = 6 + 4 = 10 cm2

Vă mulțumim că ați fost cu noi.

Perimetrul Astăzi vom vorbi despre modul de calculare a perimetrului.
Principalele linii de conținut din matematică - material geometric În acest articol terminăm ciclul "principalele linii de conținut ale cursului.
Matematica - gradul 3 Continuăm studierea subiectelor pe care copiii noștri le studiază în școala primară.
Cum să înveți un copil să navigheze în avion Copilul care se pregătește să meargă la școală ar trebui să se poată concentra asupra.
Unități de lungime Astăzi vom analiza ce unități de lungime sunt utilizate pentru măsurători. Centimetrul.

Articole similare

Pagina anterioară

Pagina următoare