O linie dreaptă este perpendiculară pe plan, dacă este perpendiculară pe orice două planuri drepte intersectate.
Cu toate acestea, este dificil să se recunoască perpendicularitatea unei linii drepte și a unui plan în general. unghiul drept este proiectat pe planul de proiecție în dimensiune completă, atunci când una dintre laturile sale este paralelă cu un plan dat de proiecții. Prin urmare, dacă într-un anumit plan å (Figura 4.19) pentru a desena doua linii intersectate, dintre care unul este orizontala h || p, iar cealaltă este frontul f || p2. apoi perpendicular pe plan å linia dreaptă a este proiectată pe planul p1 perpendicular pe h1. iar planul p2 este perpendicular pe f2.
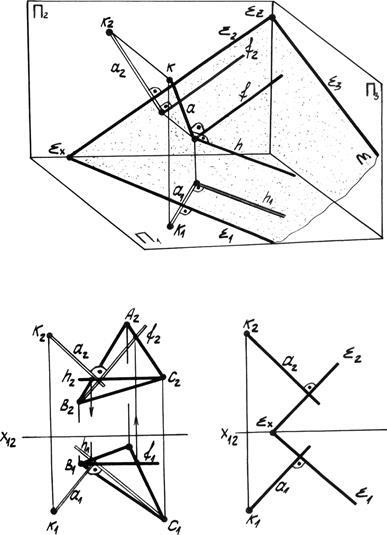
Fig. 4.19. Linie dreaptă, perpendiculară pe plan.
Deci, în cazul în care o linie dreaptă perpendiculară pe planul, proiecția orizontală este perpendiculară pe proiecția orizontală a orizontală, și punctul său de vedere frontală - perpendicular pe partea din față a proiecției frontale, precum și aceleași nume urmele.
În Fig. 4.19 cazuri de construcție a unui perpendicular de la punctul K la triunghiul ABC și la plan å, date de urme. Dacă planurile nu sunt specificate prin urme, atunci este întotdeauna necesar să se determine planul orizontal și planul frontal.
Perpendicular reciproc la plan.
Două avioane sunt reciproc perpendiculare, dacă unul dintre ele trece printr-o perpendiculare pe cealaltă.
Pentru a construi un plan perpendicular pe o anumită, este suficient să se definească o linie dreaptă perpendiculară pe ea. Prin intermediul unei perpendiculare pe plan, pot fi desenate un număr de planuri perpendiculare pe cel dat (Figura 4.20a).
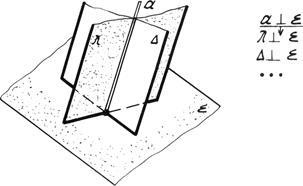
Fig. 4.20a. Perpendicular reciproc la plan.
Să considerăm construcția uneia dintre planurile perpendiculare pe planul dat (c Ç d) (Figura 4.20b).
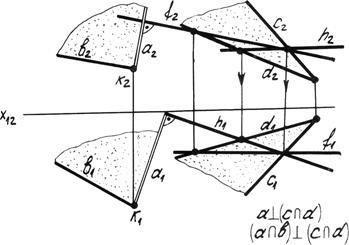
Fig. 4.20b. Perpendicular reciproc la plan.
Definim orizontala h si frontul planului dat. Din punctul arbitrar K reconstruim perpendicularul a pe proiecția orizontală a1 ^ h1. și pe proiecția frontală a2 <| 2. Finalizăm linia dreaptă a în planul liniei arbitrare b care intersectează cu ea. Planul (a Ç b) perpendicular pe plan (c Ç d).
Întrebări și probleme pentru auto-control
1. În ce mod puteți specifica un avion în desen?
2. Cum se poate proceda din orice metodă de specificare a unui avion la o metodă de specificare a urmele?
3. În ce condiții punctul și linia aparțin planului?
4. Ce linii drepte în plan sunt numite liniile principale și cum sunt îndreptate?
5. Formulează condițiile paralelismului liniei drepte a planului și condiția de paralelism a planurilor.
6. Când un unghi drept între o linie dreaptă și un plan este proiectat în dimensiune completă?
7. În ce cazuri se intersectează avioanele de-a lungul liniilor unei anumite poziții:
a) linii drepte;
b) linii de proiectare.
8. Determinați linia de intersecție a două planuri definite de linii paralele (a || b) și linii intersectate (c || d) (setate independent).
9. Se determină punctul de intersecție al liniei drepte (poziția generală) cu planul S (poziția generală).