În general, această sarcină presupune o abordare creativă, deoarece nu există o metodă universală de rezolvare a acesteia. Încercați totuși să faceți câteva inundații.
În cele mai multe cazuri, factorizarea polinomului se bazează pe corolarul teoremei lui Bezout, adică fie că rădăcina se găsește, fie că gradul polinomului este redus cu o diviziune de către. Polinomul rezultat este căutat pentru rădăcină și procesul este repetat până la descompunerea completă.
Dacă rădăcina nu poate fi găsită, se utilizează metode specifice de descompunere: de la grupare la adăugarea unor termeni suplimentari care se exclud reciproc.
Restul prezentării se bazează pe abilitățile de rezolvare a ecuațiilor de grad mai mare cu coeficienți întregi.
Punerea multiplicatorului comun din paranteze.
Începem cu cel mai simplu caz în care termenul liber este zero, adică polinomul are forma.
Evident, rădăcina unui astfel de polinom este, adică, reprezentăm polinomul sub formă.
Această metodă nu este altceva decât eliminarea factorului comun de paranteze.
Extindeți polinomul gradului trei în multiplicatori.
Evident, aceasta este rădăcina polinomului, adică x poate fi scos din paranteze:
Să găsim rădăcinile unui trinomial quadratic
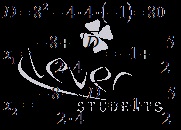
Înapoi la început
Factorizarea unui polinom cu rădăcini raționale.
În primul rând, considerăm metoda de extindere a unui polinom cu coeficienți întregi ai formei, coeficientul celei mai mari puteri fiind unul.
În acest caz, dacă polinomul are rădăcini integrale, atunci sunt divizori ai termenului liber.
Extindeți expresia.
Să vedem dacă există rădăcini întregi. Pentru a face acest lucru, scrieți divizorii de -18. . Adică, dacă un polinom are rădăcini întregi, atunci ele se numără printre numerele scrise. Vom verifica în mod constant aceste numere în conformitate cu schema lui Horner. Comoditatea lui este și în faptul că în final obținem coeficienții de extindere a polinomului:

Asta este, x = 2 și x = -3 sunt rădăcinile polinomului original și poate fi reprezentat ca produs:
Rămâne să se extindă trinomul pătrat.
Discriminantul acestui trinomial este negativ, deci nu are rădăcini reale.
.
în locul schemei lui Horner, s-ar putea folosi selecția rădăcinii și împărțirea ulterioară a polinomului într-un polinom.
Acum considerăm extinderea unui polinom cu coeficienți întregi ai formei, iar coeficientul celei mai mari puteri nu este egal cu unul.
În acest caz, polinomul poate avea rădăcini raționale raționale.
Extindeți expresia.
După schimbarea variabilei y = 2x. trecem la un polinom cu un coeficient egal cu unitatea la cel mai înalt grad. Pentru a face acest lucru, multiplicați mai întâi expresia cu 4.
Dacă funcția obținută are rădăcini integrale, atunci ei se numără printre divizorii termenului liber. Le scriem:
Calculăm succesiv valorile funcției g (y) în aceste puncte până când se obține zero.
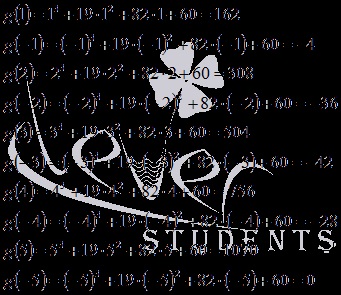
Aceasta este, y = -5 este rădăcina, prin urmare, este rădăcina funcției inițiale. Împărțim coloana (colțul) polinomului într-o binomă.
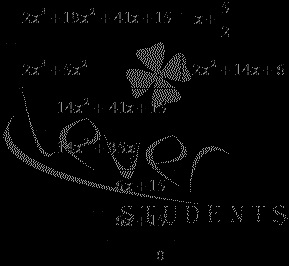
Verificarea divizoarelor rămase este inadecvată, deoarece este mai simplu să factorizăm trinomul pătrat rezultat
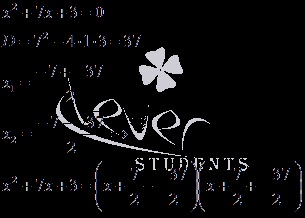
Policomalii ne-clasificate. Teorema privind descompunerea unui polinom în dobutoks nu este cunoscută. Rezultatul canonic al unui polinom.