Scurtă descriere a documentului:
Formulele de multiplicare prescurtată sunt instrumente foarte convenabile pentru operațiile cu polinoame. De regulă, acest lucru ne permite să reducem construcțiile polinomiale complexe la o expresie mică reprezentată de un binomial. Sau, într-o ordine diferită, un binomial compact este ușor derivat din produsul a două polinoame.
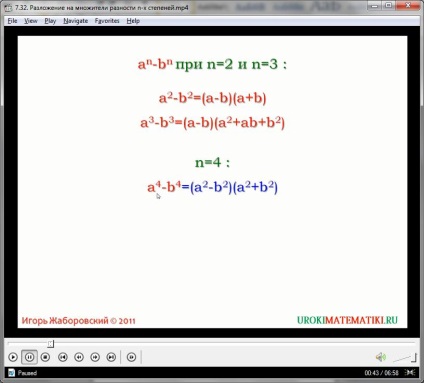
Astfel de acțiuni sunt necesare pentru rezolvarea ecuațiilor și inegalităților triviale, precum și pentru diverse probleme de probă.
Această expresie este relativ ușor de transformat prin înlocuirea expresiilor pătrate identice (x 2) 2 și (y 2) 2 pentru x 4 și y 4:
x 4 - y 4 = (x 2) 2 - (y 2) 2
Ca rezultat, obținem diferența de pătrate, care pot fi reprezentate folosind un FSU elementar ca:
(x 2) 2 - (y 2) 2 = (x 2 + y 2) (x 2 - y 2)
Pe de altă parte, a doua paranteză a expresiei care rezultă conține o diferență de pătrate, care pot fi ușor convertite:
(x 2 + y 2) (x 2 - y 2) = (x 2 + y 2) ((x + y) (x - y))
Rezultă că:
x 4 - y 4 = (x 2 + y 2) (x + y) (x - y)
Lăsăm partea comună de bază (x - y), cele două expresii rămase în paranteze se înmulțesc:
(x-y) (x + y) (x + y) (x-y) = (x-y)
Pentru ceea ce este necesar să selectați (x - y), va fi afișat mai târziu. Deci, am găsit o altă formulă pentru diferența de expresii de putere. Această ecuație este destul de greu de exprimat - dar merită să înțelegem că se potrivește logic într-o serie de formule similare pentru determinarea diferenței dintre pătrate și cuburi. Să comparăm aceste formule cu celelalte, pentru a găsi legi generale:
x 2 - y 2 = (x - y) (x + y)
x 3 - y 3 = (x - y) (x 2 + 2xy + y 2)
x 4 - y 4 = (x - y) (x 3 + x 2 y + x 2 + y 3)
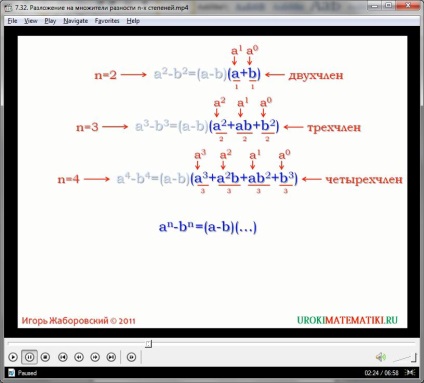
Pentru a obține o formulă generală care va ajuta la transformarea diferenței de variabile cu orice grad într-un produs de polinoame, este important să înțelegem tendințele generale din ecuațiile ordinii inițiale. Observăm că cel de-al doilea polinom din produsul nostru este suma produselor pereche de două expresii. Și gradele variabilelor sunt în relație inversă. Pentru a face mai ușor să înțelegem aceste modele, rescriem egalitatea pentru diferența de expresii de gradul 4 astfel:
x 4 - y 4 = (x - y) (x 3 y 0 + x 2 y 1 + x 1 y 2 + x 0 y 3)
Orice număr în gradul zero este în mod necesar egal cu unul. Prin urmare, pentru orice variabilă reală, putem adăuga în siguranță o construcție cu o putere de zero. Amintiți-vă că orice variabilă are un grad - dacă nu este specificat, este egal cu unul. Aceste reguli pentru manipularea de grade și a permis să prezinte egalitate într-o formă mai ușor de înțeles.
Rețineți că numărul de termeni din polinomul celor două paranteze este egal cu gradul de bază (pe care variabilele îl au în diferență). Pentru un număr de polinoame, gradul de exprimare este algebric descrescător, iar gradul celui de-al doilea se apropie. În acest caz, punctele extreme pentru puteri sunt 0 și cel mai înalt grad al diferenței inițiale dintre expresii.
Folosind aceste considerente, derivăm o formulă pentru a găsi diferența de expresie a gradului 5:
x 5 - y 5 = (x - y) (x 4 y 0 + x 3 y 1 + x 2 y 2 + x 1 y 3 + x 0 y 4)
În primul rând, vom scrie primul factor (x - y) neschimbat. Al doilea polinom va reprezenta suma celor cinci elemente (la cel mai înalt grad). Elementele, la rândul lor, sunt formate de produsul variabilelor cu o schimbare în grade algebrice, inverse și interdependente. În polinom:
x 4 y 0 + x 3 y 1 + x 2 y 2 + x 1 y 3 + x 0 y 4
x scade gradul de 4 la 0, y crește de la 0 la 4. Pentru auto-test este util să se știe că suma gradelor de orice monom, în acest caz, este egală cu toate de același cel mai înalt grad - 5.
Rămâne doar să notăm formula corect, scăpând de grade zero:
x 5 - y 5 = (x - y) (x 4 + x 3 y + x 2 y 2 + xy 3 + y 4)
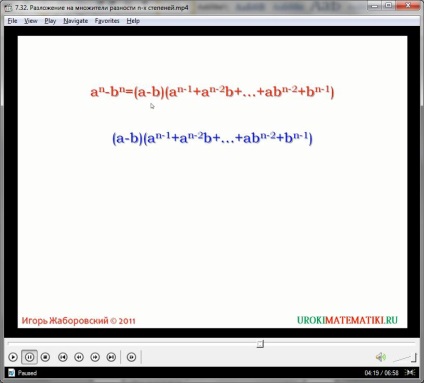
În general, pentru orice putere de n, se aplică următoarea egalitate:
(x) n - (y) n = (x - y) ((x) n + (x)
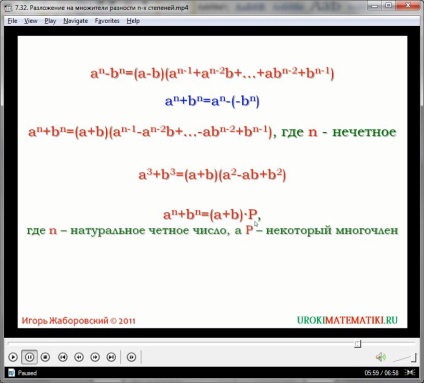
O formulă universală pentru găsirea sumei a două expresii cu diferența n este derivată prin transformarea formei:
x n + y n = xn - (-y n)
Folosind formula pentru diferența expresiilor obținute mai sus, derivăm egalitatea:
x n + y n = x n - (y n) = (x + y) ((x) n-1 - (X) n-2 ... y - x (y) n - 2 + y n-1)
Datorită faptului că piața de orice expresie elimină negativul, nu vă puteți imagina cantitatea de mijloace disponibile de pătrate (sau orice chiar grad) variabile ca produsul a două polinoame.