Teoria sistemelor automate de control
Pentru a determina stabilitatea folosind criteriul Nyquist, este posibil să se construiască o caracteristică de fază non-amplitudine, dar un răspuns de frecvență de amplitudine logaritmică (LP) și un răspuns logaritmic al frecvenței fazei (LPF) al unui sistem deschis.
Construcția l. a. x. este făcută prin exprimare
- modulul funcției de transfer de frecvență al sistemului deschis (6.23).
funcția de transfer de frecvență (6.23). Pentru a construi l. a. x. și l. f. x. Este convenabil să utilizați grila standard prezentată în Fig. 4.19.
Cea mai simplă construcție este obținută dacă funcția de transfer a unui sistem deschis poate fi redusă la forma
Faza (argumentul) funcției de transfer de frecvență
care corespunde expresiei modulului la scara logaritmică
care este de 20 dB deasupra axei abscise.
punctul A scade la 40 dB.
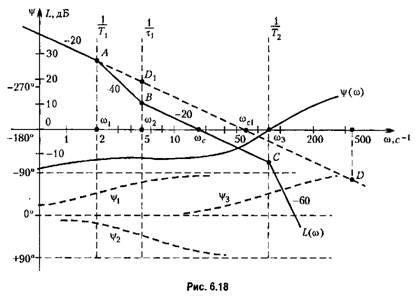
factor de ordinul doi al numitorului (6.28), apoi n. a. x. rupe la -40 dB / dec și ultimul asymptot va avea o panta de -60 dB / dec.
- cu 6 dB mai mică decât cea asimptotică.
Expresia pentru faza (6.28) are forma
(vezi figura 6.18). Toate celelalte sunt obținute printr-o deplasare simplă a acestei caracteristici de fază, astfel încât să aibă o schimbare de fază de 45 ° la frecvența de potrivire corespunzătoare. Este necesar să se ia în considerare semnul fiecărui termen (6.30). Caracteristica fazei logaritmice (Figura 6.18) este obținută ca urmare a însumării algebrice a tuturor termenilor (6.30). Construcția l. f. x. poate fi mult simplificat dacă se pregătește un șablon pentru una dintre dependențele specificate.
O construcție similară. a. x. și l. f. x. poate fi făcută pentru orice valoare a lui r. Diferența constă în panta primei asimptote a lui n. a. x. și valoarea primului termen al expresiei pentru faza (6.27).
Pe primul litru. a. x.
în asimptoticul n. a. x. ar trebui să fie modificată în conformitate cu Fig. 4.15 sau Fig. 4.16 (pentru primul dintre acești factori sunt luați cu semnul opus).
În același mod ca mai sus, f. x. Pentru a construi componentele caracteristicii de fază, corespunzătoare factorilor cu rădăcini complexe, putem folosi graficele prezentate în Fig. 4.15.
Acum ne îndreptăm atenția spre investigarea stabilității unui sistem închis construit de n. a. x. și l. f. x. sistem deschis. Pentru a face acest lucru, vom folosi ultima formulare de mai sus a criteriului Nyquist asociat cu trecerea lui a. f. x. prin segmentul critic.
. Ca și înainte, o tranziție de sus în jos este considerată pozitivă, iar o tranziție de jos în sus este negativă.
tranziția prin segmentul critic apare și sistemul închis devine instabil.
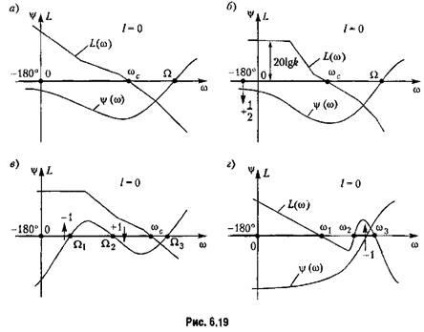
iar suma tranzițiilor este zero.
Deoarece există o trecere prin a doua parte a segmentului critic, sistemul închis este instabil.
Marele avantaj practic al criteriului Nyquist este acela că: a. f. x. sau l. h. x. sistemele deschise pot fi obținute nu numai prin calcul (inclusiv prin folosirea mijloacelor informatice) pentru o anumită funcție de transfer a unui sistem deschis, dar și eliminate în mod experimental în prezența unui sistem automat deja creat ca întreg sau a dispozitivelor sale individuale. Acest lucru este deosebit de important atunci când fiabilitatea ecuațiilor diferențiale inițiale este îndoielnică pentru un motiv sau altul.