4. Cerc numeric
Să specificăm ce este un cerc numeric și care sunt relațiile dintre setul de puncte dintr-un cerc și setul de numere reale.
Originea contorului este punctul A. Direcția invers acelor de ceasornic în sens invers acelor de ceasornic este pozitivă, direcția în sensul acelor de ceasornic este negativă. Scala este lungimea cercului (Figura 4).
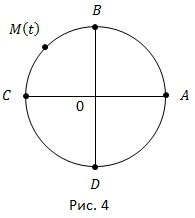
Introducând aceste trei poziții, avem un cerc numeric. Să indicăm cum să atribuiți fiecărui număr un punct al cercului și viceversa.
Având un număr, obținem un punct pe cerc
Fiecare număr real corespunde unui punct din cerc. Și dimpotrivă?
Punctul corespunde unui număr. Și dacă luați numerele Toate aceste numere au doar un punct pe cercul lor
De exemplu, aceasta corespunde punctului B (figura 4).
Luăm toate numerele, toate corespund punctului B. Nu există o corespondență unu-la-unu între toate numerele reale și punctele cercului.
Dacă există un număr fix, atunci doar un punct din cerc corespunde cu acesta
Dacă există un punct de cerc, atunci acesta corespunde unui set de numere
Spre deosebire de o linie dreaptă, cercul de coordonate nu are o corespondență unu-la-unu între puncte și numere. Pentru fiecare număr corespunde doar un punct, dar pentru fiecare punct există un număr nenumărate de numere și le putem scrie.
5. Punctele de bază ale unui cerc
Luați în considerare punctele principale ale cercului.
Se dă un număr pentru a găsi punct la care corespunde.
Împărțind arcul la jumătate, obținem un punct (Figura 5).
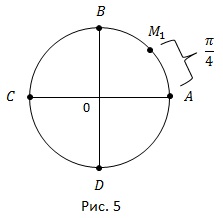
Problemă inversă - punct intermediar punct al unui arc Găsiți toate numerele reale care corespund acesteia.
Notați cu cercurile numerice toate arcele care sunt multiple (Figura 6).
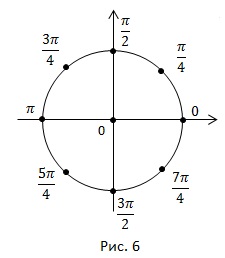
De asemenea, sunt importante arce, multiple
Având în vedere numărul de care aveți nevoie pentru a găsi punctul adecvat.
Problema inversă are un punct, este necesar să găsim cu ce numere corespunde.
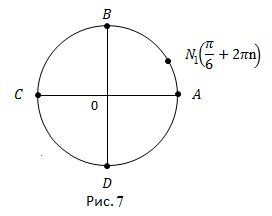
Am examinat două probleme standard la două puncte critice.
a) Găsiți pe un cerc numeric un punct cu o coordonată
Am amâna două rotații întregi din punctul A și o jumătate, și obținem punctul M - acesta este mijlocul celui de-al treilea trimestru (Figura 8).
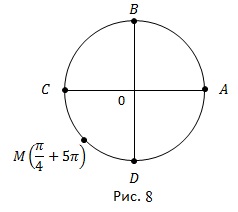
Răspuns. Punctul M este mijlocul trimestrului al treilea.
b) Găsiți un punct cu o coordonată pe cercul numeric
Părăsim o întoarcere completă din punctul A și obținem și punctul N (figura 9).
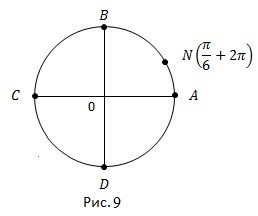
Răspuns: Punctul N este în primul trimestru.
7. Concluzie, concluzie
Am considerat o linie dreaptă numerică și un cerc numeric, amintit de trăsăturile lor. Singularitatea liniei de numere este o corespondență unu-la-unu între punctele acestei linii și setul de numere reale. Nu există o astfel de corespondență unu-la-unu în cerc. La fiecare număr real din cerc corespunde un singur punct, dar la fiecare punct al cercului numeric corespunde un număr infinit de numere reale.
În următoarea lecție, vom lua în considerare un cerc numeric în planul de coordonate.