Scop. Pentru a clarifica în practică că obiectele (obiecte, fenomene, procese) pot avea proprietăți speciale, numite cantități. Principalele prevederi asociate cu cantități omogene, utilizate pentru a rezolva problemele de matematică în școala primară.
Întrebări de studiu
Conceptul de o cantitate scalară pozitivă și măsurarea acesteia.
Acțiuni cu cantități scalare pozitive.
Măsurarea cantităților în practică.
Unități standard de cantități.
Concepte de bază ale temei
cantitate scalară pozitivă;
Principalele concluzii teoretice
Obiectele (obiecte, fenomene, procese) pot avea proprietăți speciale, numite cantități.
Proprietatea ar putea fi considerată o valoare dacă îndeplinește o serie de condiții:
Pentru cantitățile din același gen, au loc relațiile "egale", "mai puțin" și "mai mare", iar pentru orice valori ale lui A și B, este valabilă numai una dintre relații: A , , .
Raportul "mai mic" pentru cantitățile omogene este tranzitoriu:
Dacă A și B C, atunci A C.
Pot fi adăugate valori de un fel, ca urmare a adăugării, se obține o cantitate de același fel. Cu alte cuvinte, pentru oricare două cantități A și B, cantitatea C = A + B, numită suma cantităților A și B, este determinată în mod unic.
Valorile de un fel pot fi scăzute, rezultând în valoarea de același fel. Determinați scăderea prin adăugare.
Diferența dintre A și B este o cantitate C = A-B astfel încât A = B + C.
Diferența dintre A și B există dacă și numai dacă A B.
Valoarea poate fi înmulțită cu un număr real pozitiv, rezultatul fiind o valoare de același fel. Mai exact, pentru orice cantitate A și orice număr real pozitiv x există o cantitate unică B = x A, numită produsul lui A cu numărul x.
Valorile de un fel pot fi împărțite, rezultând într-un număr. Determinați diviziunea prin înmulțirea valorii cu un număr.
O valoare particulară a lui A și B este un număr real pozitiv x = A astfel încât A = x B
Valorile ca proprietăți ale obiectelor se manifestă atunci când sunt comparate, iar pentru fiecare valoare există o modalitate de comparație. Dacă este selectată o unitate de mărime, valoarea poate fi măsurată. Ca rezultat al măsurării, se obține un număr, care se numește valoarea numerică a unei cantități sau o măsură a valorii pentru o unitate de măsură selectată.
Se introduc intrările X = a, D și a = m (X), unde X - reprezintă o cantitate, este o unitate de mărime și a este un număr real.
Care sunt valorile din următoarele propoziții:
a) Perele sunt mai scumpe decât merele.
b) Cartea este mai grea decât un notebook.
c) Tanya deasupra Sveta.
Ce valori pot caracteriza următoarele obiecte:
a) un creion; b) persoana; c) Lacul?
Există două bucăți de sârmă. Cum puteți compara lungimea lor fără a recurge la măsurare? Care pot fi rezultatele comparației?
Cum putem compara masele a două obiecte fără a determina masa fiecăruia dintre ele? Care pot fi rezultatele comparației?
Figura 1 prezintă două dreptunghiuri având zonele A și B.
Construiți un dreptunghi a cărui arie este: a) A + B; b) 3A; c)
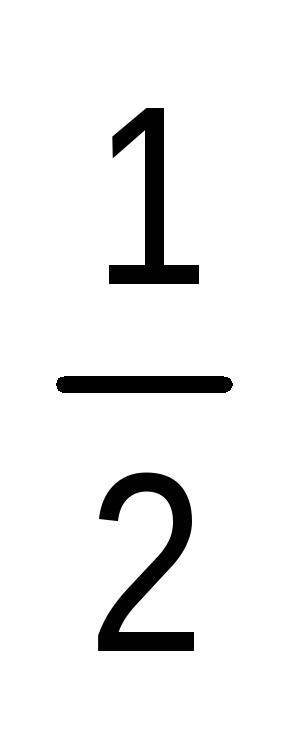
Împărțiți în clase în trei moduri următoarele valori:
A este înălțimea copacului; M - suprafața consiliului;
C este masa plăcii; K - 26 m;
D = 25 cm; L este lungimea frânghiei;
E este vârsta pomului; P este grosimea plăcii.
Denumiți unitățile standard cu care puteți măsura valorile afișate în tabel. Scrie-le jos.