STUDIUL INERTIEI ELLIPSOID A SOLIDELOR CU OSCILLĂRI DE TORSION
Momentul de inerție al unui corp rigid în raport cu o axă este cantitatea:
unde dm este elementul de masă al corpului,
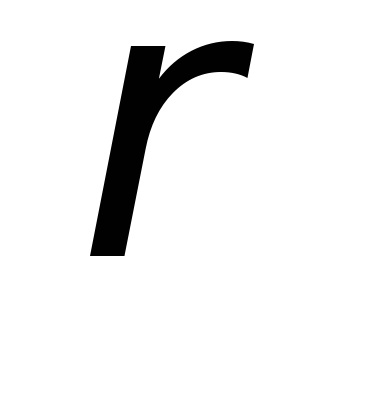
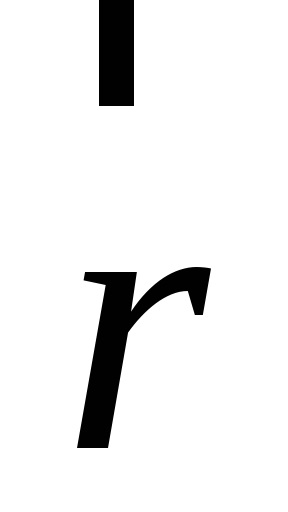
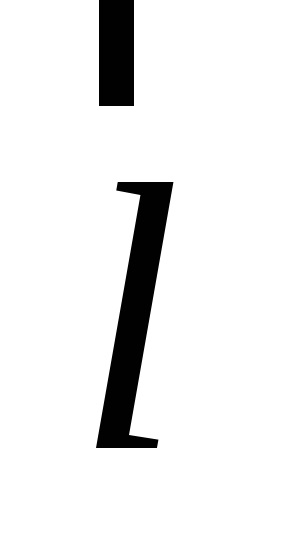
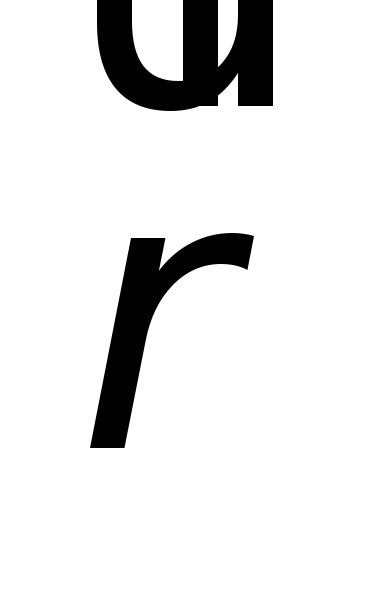
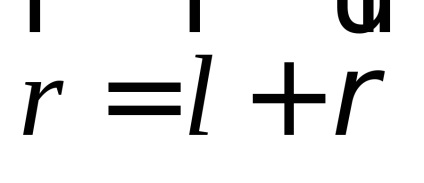
Înlocuirea valorii găsite
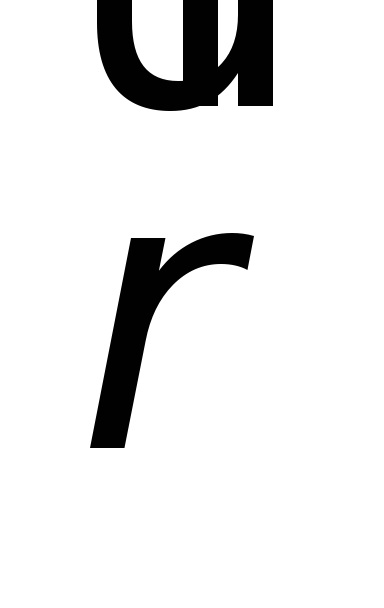
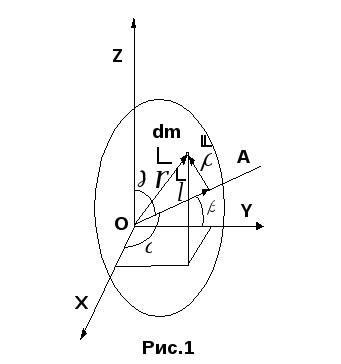
Exprimăm r2 și 12 în ceea ce privește coordonatele x, y și z ale elementului dm. a1 prin aceleași coordonate și direcții cosinuse ale axei OA:
l = x cos α + y cos β + z cos γ.
În mod similar, procedăm cu y2 și z2. Formula (2) ia forma:
În această expresie se utilizează următoarea notație:
,,
,.
Este ușor de observat că cantitatea Ixx este momentul de inerție în raport cu axa Ox, respectiv Iyy iIzz - momentele de inerție în ceea ce privește oseyOy iOz. Cantitățile Ixy, Ixz și Iyz sunt numite momente centrifuge de inerție. După cum rezultă din formula (3), pentru a determina când rotirea unui corp rigid în raport cu o direcție arbitrară a axei trebuie să cunoască cosinusului direcția axei în raport cu selectată de sistem și cele șase cantitățile de coordonate - Ixx, Iyy, Izz, IXY, Ixz, Iyz. calculată în același sistem de coordonate.
Formula (3) admite o interpretare geometrică simplă. Din originea coordonatelor de-a lungul axei OA se scade un segment
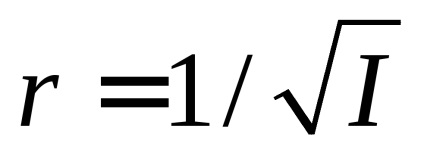
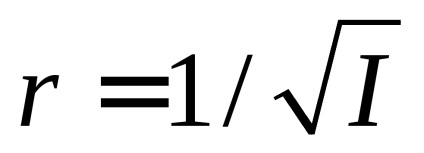
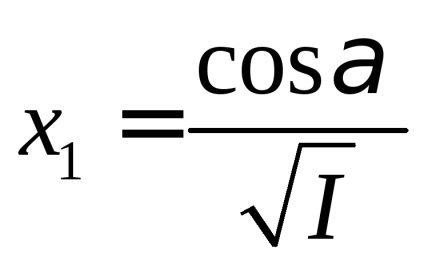
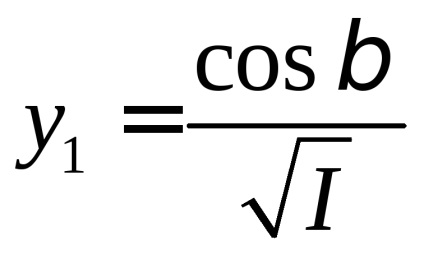
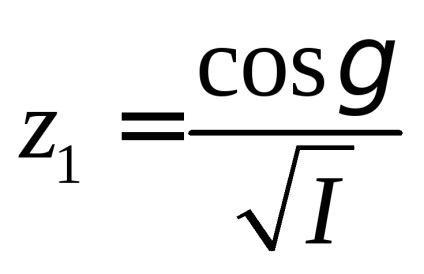
Exprimând cosá, cosβ, cosγ din aceste egalități și plasând expresiile găsite în formula (3), ajungem că suprafața cerută este descrisă de ecuația:
Această ecuație definește o suprafață de ordinul doi, care în acest caz este un elipsoid, deoarece toate segmentele lui r au valori finite. Elipsoidul corespunzător este numit elipsoidul de inerție în raport cu punctul O. Punctul O este numit centrul său.
Scopul lucrării propuse este studiul experimental al elipsoidelor de inerție a solidelor.
Atunci când poziția originii O se schimbă în raport cu corpul, elipsoidul inerției se schimbă, de asemenea. Dacă punctul O coincide cu centrul de masă al corpului, atunci elipsoidul corespunzător de rotație se numește central. Forma elipsoidului de inerție depinde, desigur, numai de proprietățile corpului și de alegerea punctului despre care este investigat elipsoidul de inerție și nu depinde de alegerea axelor. Cu toate acestea, forma ecuației care descrie elipsoidul inerțial depinde în mod esențial de direcția axelor. Mai ales, ecuația elipsoidului de inerție este exprimată într-un sistem de coordonate ale cărui axe sunt direcționate de-a lungul axelor principale ale elipsoidului de inerție. În acest sistem de coordonate, toate momentele centrifuge dispar și ecuația elipsoidului de inerție ia forma:
,
și expresia momentului de inerție a corpului în raport cu axa cu direcțiile cosinelor
In multe cazuri de importanță practică direcția axelor principale de simetrie folosind distribuția masei poate fi determinată în corpul elipsoidului de inerție: fiecare plan de simetrie este un plan de simetrie al elipsoidului de inerție; Normalul acestui plan determină una dintre axele principale ale elipsoidului. De exemplu, axa mare a elipsoidului de inerție al unui paralelipiped dreptunghiular uniform sunt paralele cu marginile sale. Dacă corpul are o simetrie de rotație în jurul unei axe, atunci elipsoidul său de inerție are aceeași simetrie. Axa de rotație a simetriei corpului este una dintre axele principale. Orice linie dreaptă perpendiculară pe această axă este, de asemenea, axa principală a elipsoidului. Rețineți că simetria elipsoidului de inerție poate fi nu numai egal, dar de multe ori este mult mai mare decât simetria corpului. Astfel, elipsoidului inerției are forma unui elipsoid de revoluție nu numai un cilindru, ci și un pătrat și la prisma hexagonala drept și, în general, în toate cazurile, atunci când axa trec prin mai mult de două planuri de simetrie.
În mod similar, elipsoidul de inerție ia forma unei mingi nu numai pentru o distribuție masică simetrică sferică, ci și, de exemplu, cu simetrie cubică a corpului. Nu este greu să ajungem la această concluzie, observând că cubul are mai multe planuri de simetrie decât pentru corpurile care au un elipsoid de inerție sub forma unui elipsoid de revoluție. În acest caz, orice axă neutră, i. E. Axa care trece prin centrul de masă este axa principală de inerție.
În această lucrare, elipsoidul inerției unui corp solid este studiat prin metoda oscilațiilor torsionale. Corpul de încercare este întărit într-un cadru special (vezi figura 3). Rama este suspendată pe un fir metalic pe un suport prevăzut cu o pârghie, prin care poate comunica vibrațiile de torsiune în raport cu axa verticală. În ceea ce privește corpul investigat, se utilizează un paralelipiped de textolit. În centrul fețelor paralelipipedului, în mijlocul marginilor sale și la vârfuri, se fac mici indentări pentru fixarea în cadru.
Luați în considerare oscilațiile sistemului în cazul în care axa de rotație trece de-a lungul uneia dintre diagonalele principale ale paralelipipedului, de exemplu, diagonala OA (figura 2). În acest caz, paralelipipedul este întărit în cadru prin vârfurile A și C. Ecuația de mișcare a sistemului are forma:
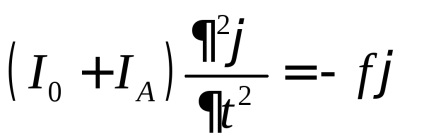
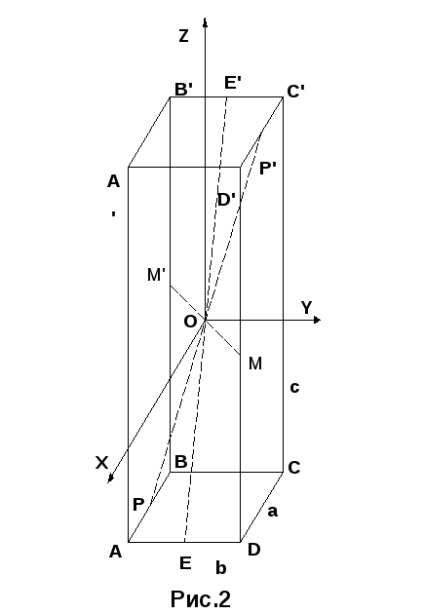

Perioadele de oscilații ale sistemului față de axele principale ale paralelipipedului (din raționamentul precedent este clar că aceste axe trec prin centrele unor fețe opuse) sunt egale:
Lăsați dimensiunea paralelipipedului de-a lungul axei Ox să fie egală. de-a lungul axei Oy este egală cu b. de-a lungul axei Oz-c. Pătraturile direcției cosinilor diagonale sunt egale cu:
Exprimându momentyIA, Ix0, Iy0, Iz0 prin perioade de vibrație folosind relațiile (7) și (8), înlocuind valorile obținute și valorile cosinus direcție (9) în ecuația (6), atunci obținem:
Această relație este verificată experimental.
Relațiile analoge relaționează perioadele Tx, Ty, Tz cu perioadele de oscilație ale sistemului față de axele care leagă punctele medii ale marginilor paralelipipedului:
Studentul este încurajat să deducă aceste relații în mod independent și să le testeze experimental.
Pentru cub, relațiile (10) - (11) reduc la egalitatea perioadelor de oscilație față de orice axă care trece prin centrul cubului.
Citiți instalarea. Verificați dacă dispozitivul funcționează pentru a excita vibrațiilor de torsiune nu apar în cazul în care vibrațiile cadru laterale în plan vertical (în cazul în care acestea apar, se reduce amplitudinea lor țineți ușor de rama de sârmă sau manual).
Măsurați perioadele de oscilație ale sistemului în jurul axelor corespunzătoare axelor principale ale elipsoidului de inerție a paralelipipedului. Pentru a face acest lucru, întăriți cutia în cadru cu ajutorul canelurilor situate în centrele fețelor opuse.
Corpul este fixat în cadru după cum urmează: eliberați mai întâi bara mobilă 1 (Figura 3) prin deșurubarea piulițelor 2 și 3 ale cusăturilor laterale. să acorde o atenție, astfel, la poziția șurubului de prindere 4: capătul inferior reliefează benzi de 5-7 mm. Apoi, ridicând bara 1 de-a lungul ghidajelor 5 și 6 și ținându-l de mână, setați corpul de test, astfel încât o degajare corespunzătoare a intrat în proiecția 8 pe partea inferioară a cadrului de bara transversală, apoi inferior șinei 1 de-a lungul ghidajului (proeminența șurubul de fixare 4 trebuie să intre în locașul opus suprafață corporală), fixați piulițele 2 și 3 și mânere laterale ale corpului cu șurub ușor podozhmite 4 (fără a aplica o forță excesivă). Apoi exciti vibrațiile de torsiune ale sistemului și vedeți dacă rama se rotește în raport cu corpul. Dacă este necesar, strângeți mai mult șurubul de fixare.
Stabiliți domeniul de funcționare al amplitudinii de oscilație a sistemului. Având excitat în oscilațiile de torsiune ale sistemului, măsurați timp de 10-15 fluctuații complete și găsiți perioada T1. corespunzătoare unei anumite valori inițiale a amplitudinii
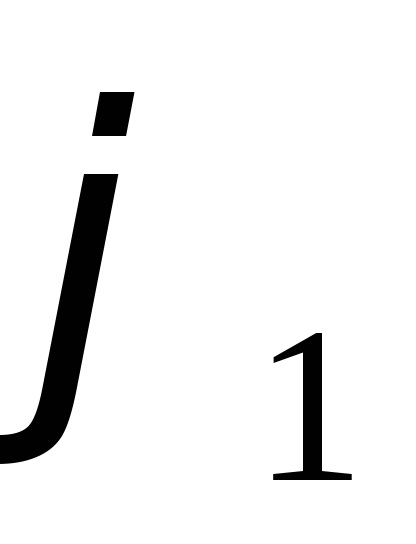

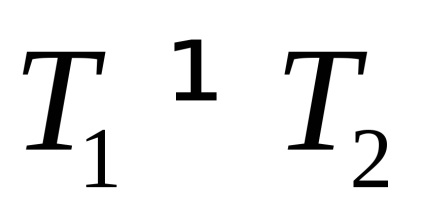
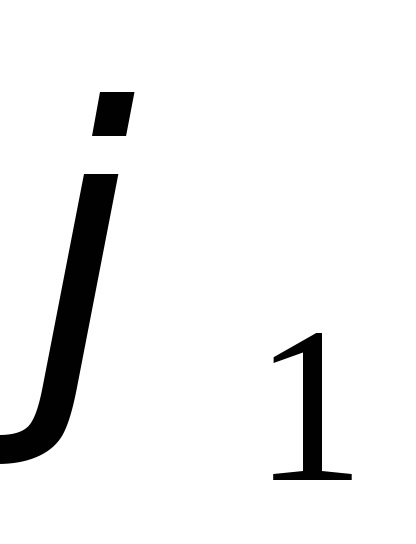
Verificați validitatea (10). Pentru a face acest lucru, întăriți cutia în așa fel încât axa de oscilație să coincidă cu una din diagonalele principale ale paralelipipedului și să măsurați perioada de oscilație a sistemului. Măsurătorile trebuie efectuate pentru fiecare diagonală. Măsurați timpul de 10-15 oscilații, repetând fiecare măsurătoare de cel puțin trei ori. Măsurați dimensiunile geometrice ale paralelipipedului cu ajutorul etrierului.
Verificați valabilitatea formulelor (11) prin măsurarea perioadelor de oscilații ale sistemului în raport cu axele care trec prin punctele medii ale marginilor.
Desenați elipsoidul inerției paralelipipedului. Pentru a face acest lucru, trageți mai întâi secțiunile elipsoidului de către planurile Oxy, Oxz și Oyz. Construiți construcția după cum urmează. Măsurați perioada de oscilație a cadrului gol T0 și trasați segmentul Ri de-a lungul axei corespunzătoare. proporțională
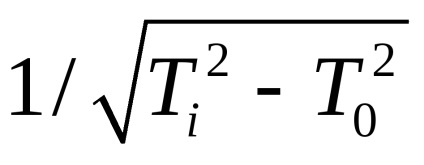
Explorați elipsoidul inerției cubului, măsurând perioadele de oscilație a cadrului cu cubul.
Sivukhin D.V. Cursul general al fizicii, vol. 1. Mecanică. M. Science. 1974, §§ 53, 54.
Strelkov S.P. Mecanică. M. Science. 1975, §§63, 64.