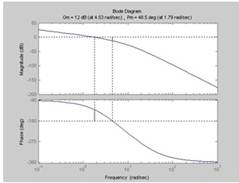
Se compară caracteristicile logaritmice ale unui sistem deschis folosind MATLAB (operatorul punct sau marginea). 1.3 a.
Se compară graficul AFCS utilizând MATLAB (operatorul nyquist) din Fig. 1,3 b pentru un sistem deschis.
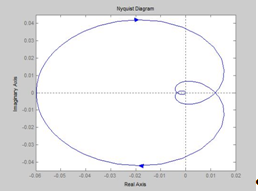
Rezervele de modulo și de fază de stabilitate sunt determinate de caracteristicile logaritmice (vezi Figura 1.3a): la frecvența cutoff wc, marja de fază este determinată - # 8710; # 966; și marja în amplitudine # 8710; L - la frecvența la care (W) = -180. În acest fel, # 8710; L≈0. 1dB, # 8710; # 966; ≈ 0 °, care este inadecvată.
4. Mărimea erorii de viteză este definită ca esk = V1 / K. Pentru o estimare aproximativă a tnn și # 963; este necesar să se construiască un proces tranzitoriu h (t) (operatorul pas în MATLAB) pentru v (t) = 1 [t], iar din acesta să se determine tnn și # 963;
Pentru a obține ecuațiile de stări în formă normală, folosim ecuația diferențială a unui sistem închis
D (s) y (t) = Kv (t). Dacă D (s) = b0s4 + b1s3 + b2s2 + b3s + b4 = 0. atunci ecuația de stat are forma
Pentru a descrie sistemele dinamice în spațiul de stare, Matlab utilizează modele ale subclaselor ss care se bazează pe ecuații diferențiale sau diferențiale liniare.
Modelul unui sistem continuu în subclasa ss are forma:
unde: x este vectorul de stare; v - vector de intrare; y este vectorul de ieșire.
Pentru a forma modele în subclasa ss, funcția ss
Ca rezultat, sub denumirea sys, primim un ss-obiect cu caracteristici numerice sub forma a patru matrici, care trebuie să aibă dimensiuni convenite. În acest caz, matricea D este setată la 0.
Pentru a construi procesul tranzitoriu h (t), vom folosi operatorul pas în MATLAB.
Implementarea funcțiilor arată astfel:
sys = ss ([0 1 0 0, 0 0 1 0, 0 0 0 1; -B4 / b0 B3- / b0 -B2 / b0 -b1 / b0], [0 0 0 K / b0]“, ochi ( 4), zerouri (4,1))
Ca rezultat, obținem graficul prezentat în Fig. 1.4. Vom fi interesați de Out (l). Rata de eroare este definită ca:
esc = V1 / K = 1,4 / 3,243 = 0,432> esc = 0,04.
Pentru o estimare aproximativă a tnn și o, un proces tranzitoriu h
Timpul procesului tranzitoriu este determinat ținând seama de următoarele relații: (T) / (l + K), unde v (t) = 1 [t] și K = 3.243 este coeficientul total de transfer al sistemului deschis. Apoi ey = 1 / (1 + 3,243) = 0,236 și deci tnp din graficul Out (l) tpp ≈50c> tppad = 2,5 s.
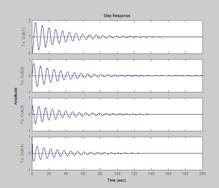
Astfel, sistemul inițial nu satisface indicatorii de calitate dat, trebuie corectat.
5. Dacă sistemul sursă nu respectă indicatorii de calitate specificați, acesta trebuie ajustat. În cazul aplicării metodelor de sinteză a corecției, LACHH Lzh (w) dorit este construit. Porțiunea de joasă frecvență, menținând în același timp astatism comanda LACHH dorit (integrator prezența 1 / s în sistem) selectează câștigul dorit din raportul Kz = v1 / Esk = 1,4 / 0,04 = 35. La LACHH frecvență de tăiere de dorit să aibă pantă de -20 dB / decadă cu lungimea acestei secțiuni nu mai puțin de un deceniu. Alte colegii porțiune de gama medie LACHH cu segmentul de linie de joasă frecvență, cu pantă -40 (dacă este necesar -60) dB / decadă, iar partea de înaltă frecvență a sursei dorite și ar trebui să coincidă LACHH întâmplare.
Contabilizarea cerințelor de calitate ale procesului tranzitoriu: tpp și # 963; stocurile de stabilitate sunt luate în considerare la formarea regiunii de frecvență medie Lzh (w). Aici puteți utiliza graficul (Figura 1.5).
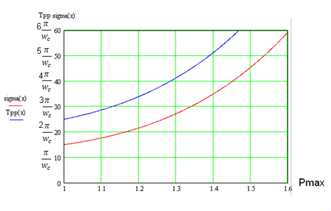
Conform graficului din Fig. 1.5 pentru valori date de y și tnn, găsim wn și apoi de la raportul wc = (0.6-0.9) wn, frecvența de cutoff wc.
În cazul nostru: (așa cum se arată în figura 1.5) pentru y = 10%, tp = 3π / # 969; n, pentru care pentru tp valoarea N = 3π / 1,5 = 6,8 1 / s și C = 5 1 / s.
Conjugarea porțiunea mijlocie cu frecvență joasă și de înaltă frecvență (fig. 1.6) trebuie să fie astfel încât a fost mai ușor să kinks și corectare, dacă este posibil, să nu fie mai mare de 20 dB / decadă (porțiunea de lungime de aproximativ zece zile). Apoi, alegeți L2≈10dB la frecvență # 969; 2 = (0,1-0,5) # 969; c = 2,5<ωс=5 и L3≈ -10 дБ на частоте ω3=25 ≥ ωс=5. Введем обозначения:
Suma Se constată din condiție că valorile Lg (# 969; 1) = Lixx (# 969; 1) sunt egale. Asta este
relația conduce la următoarea expresie:
Ultima expresie indică:
Ultimele două cantități se găsesc din expresia pentru Lixx (w).
Valoarea găsită de formula # 969; 1 = 0,098
LACH-ul dispozitivului de corecție cu caracteristică Lk (w) corespunde funcției:
Funcția generală de transfer a sistemului deschis cu o legătură corectivă de tip secvențial are forma:
În continuare, vom folosi funcția ZPK (z, p), unde z și p - vector de zerouri și poli, un Kd - un raport de transmisie generic, sys - orice nume atribuit modelului. Apoi intrarea în sistemul Matlab va arăta astfel:
sys1 = zk ([- 1 / t2k -1 / t3k], [0-1 / t1-1 / t2-1 / t3-1 / t1k -1 / t4k]
s (s + 7,143) (s + 4,167) (s + 25) (s + 0,4762) (s + 0,097)