Soluția. Introducem înlocuirea liniară (5.8), alegând C1 = 0, h1 = 0.5; C2 = 0,10, h2 = 10-2.
Calculam estimările așteptărilor matematice prin formula (3.7).
Obținem estimări imparțiale ale varianțelor cu formula (3.8).
Calculul estimării covarianței se realizează utilizând formula (5.9).
Căutăm evaluarea coeficientului de corelație cu formula (5.10).
Ecuația selectivă de regresie liniară a lui Y pe X.
.
sau y = 0,0978 = -0,00678 (x + 0,278).
Ecuația selectivă de regresie liniară a lui X pe Y.
.
sau y = 0,0978 = -0,0122 (x + 0,278).
Regresiile directe sunt prezentate în Fig. 1, există, de asemenea, puncte experimentale.
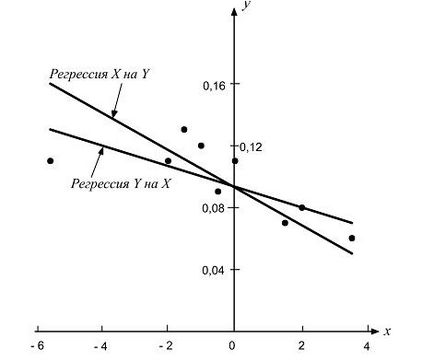
Fig. 1. Dependența modificării concentrației de azot din oțel (y)
când este descărcat de la convertizor din concentrația inițială de carbon (x)
Conform nomograms (vezi figura 1 din apendicele din [1]) pentru valoarea r = -0.746 (n = 9) găsim intervalul: - 0.95 <ρ <– 0,14. Так как значение ρ = 0 не принадлежит найденному доверительному интервалу, гипотеза о существовании линейной зависимости не противоречит экспериментальным данным с уровнем значимости α = 0,05.
Să verificăm ipoteza că nu există o dependență liniară între valorile X și Y utilizând criteriul (5.13). Conform tabelului cuantic al distribuției Studentului, găsim t0.975 (7) = 2.365. Noi calculam
.
Deoarece | r | = 0.774> 0.667, acceptăm ipoteza existenței unei relații liniare între valorile X și Y.
Rezultatele obținute permit să se concluzioneze că, odată cu creșterea uneia dintre valori, valoarea medie a celeilalte cantități scade. Deoarece coeficientul de corelație este semnificativ, se pot folosi ecuațiile liniilor de regresie selectivă pentru a prezice valoarea medie a unei variabile de la valoarea celeilalte.
Într-un raport referitor la un calcul tipic, ar trebui prezentate toate calculele efectuate, ecuațiile regresiei directe a eșantionului. În desen, ar trebui să fie prezentate ecuațiile de regresie directă, în același loc toate punctele experimentale ar trebui marcate. În concluziile formulate rezultă testarea ipotezei privind prezența (absența) unei relații liniare între variabilele aleatoare. Dacă se acceptă ipoteza existenței unei relații liniare, se trasează o concluzie cu privire la puterea și caracterul relației dintre valorile X și Y.
Precizia de calcul a evaluărilor așteptările - semn alternativ în comparație cu datele originale, estimări ale varianța, abaterea standard, covarianță - trei cifre semnificative, coeficientul de corelație estimat - trei zecimale.
Ordinea lucrării:
1. Calculați estimările așteptărilor matematice ale variabilelor aleatoare X1 și X2. elemente de estimare a matricei de covarianță: variante și covarianță. Pentru a simplifica calculul și organizarea controlului, se recomandă codarea datelor, așa cum sa făcut în 10.3. Controlul computațional este asigurat prin repetarea calculului cu alte puncte de referință. Rezultatele trebuie să corespundă eventualelor erori de rotunjire.
2. Calculați estimarea coeficientului de corelație.
3. Folosind nomograma ([1], p.83), găsiți intervalul de încredere pentru coeficientul de corelație, testați ipoteza existenței unei relații liniare între X1 și X2.
4. găsiți ecuațiile liniilor de regresie empirică X2 pe X1 și X1 pe X2. Construiți aceste linii într-un singur desen. Aplicați aceleași puncte experimentale pe același grafic.
5. Să tragă o concluzie cu privire la puterea și caracterul legăturii dintre X1 și X2.
1. Karasev V.A. Rumshinsky L.Z. Organizarea experimentului. -M. MISiS, 1986, N105, p. 74-78.