Alături de parametrii primari discutate mai sus (coeficienți în sistemele de ecuații) cuadripol, soluția multor probleme sunt caracteristice (secundare) parametrii quadropol. Acestea includ: impedanța caracteristică, un transfer constant (măsura de transfer) și raportul de transformare.
Este cunoscut faptul că generatorul cu rezistență internă Zi oferă ZH maximă de încărcare de putere furnizate Zi = ZH. Dacă între generator și sarcina este cuadripol, atunci pentru transferul maxim de putere de la generator la quadrupole necesare pentru a coordona rezistența de intrare a ZBX1 cuadripol cu impedanță internă a generatorului pentru a satisface condiția care este Zi = ZBX1. și de a transmite puterea maximă de la rețeaua cu patru terminale la sarcină # 63; se potrivesc impedanța de ieșire a portului cu patru porturi cu rezistența la sarcină, adică pentru a îndeplini condiția ZBX2 H = Z. Modul de funcționare a rețelei cu patru terminale, atunci când Zi = ZBX1 și ZBX2 H = Z, se numește modul de includere coordonată.
Se pare că pentru orice rețea cu patru terminale există o pereche de rezistențe pentru care condiție
Aceste rezistențe sunt denumite impedanțele caracteristice ale rețelei cu patru terminale și sunt notate de Z1C și Z2C.
Rezolvând aceste ecuații împreună, găsim:
Deoarece impedanțele caracteristice pot fi exprimate prin parametrii de ralanti și scurtcircuit:
Dacă terminalul 4 este adaptat încărcării, adică
atunci ecuațiile din sistemul A-parametru au următoarea formă:
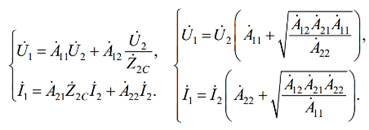
Din ultimul sistem de ecuații se poate obține
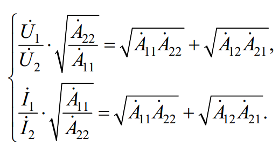
Valoarea se numește coeficientul de transformare al rețelei cu patru terminale.
Impedanța de intrare a cvadripolului corespunzător:
și anume cvadripolul corespunzător transformă rezistența de sarcină în (nT) de 2 ori.
unde g este constanta caracteristică a transmisiei (măsura de transmisie) a rețelei cu patru terminale.
adică constanta de transmisie este determinată numai de parametrii primari ai rețelei cu patru terminale.
Exprimăm parametrii primari A prin parametrii caracteristici
Conform celor de mai sus:
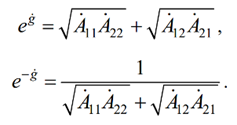
Înmulțind numărul și numitorul ultimei expresii cu. și având în vedere acest lucru. obținem:
unde ch g este cosinus hiperbolic, sh g este un sinus hiperbolic.
Ca rezultat, obținem un sistem de ecuații care conectează parametrii primari cu cei secundari,

Substituind coeficienții din ecuațiile pentru A - parametri, obținem un sistem de ecuații în caracteristicile quadropol hiperbolic:
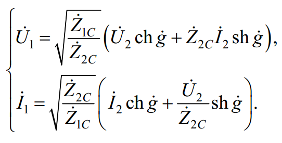
Dacă rețeaua cu patru terminale este simetrică Z1C = Z2C.
Cu o încărcătură convenită, ZH = Z2C, Z2C I2 = U2. ch g + sh g = e g sistemul de ecuații ia forma:
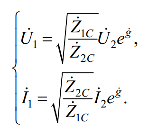
Constanta de transmisie în cazul general este valoarea complexă g = a + jb.
Rezistențele caracteristice sunt și cantități complexe
Amplitude sau valori efective ale tensiunilor și curenților la intrare și ieșire legate printr-o caracteristică de rezistență cuadripol și o transmisie constantă următoarele expresii:
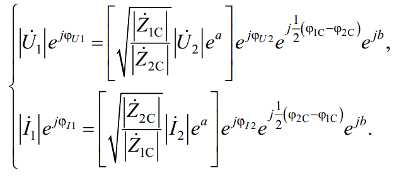
Astfel, partea reală a transmisiei constante caracterizează modificarea amplitudinii sau a valorii curente a curentului și a tensiunii când semnalul trece prin rețeaua de patru terminale. Componenta imaginară b caracterizează schimbarea de fază între tensiunile sau curenții de intrare și ieșire
Pentru o rețea simetrică cu patru terminale:
b - coeficient de fază - măsurat în radiani sau grade și egal cu
Coeficientul a este o amortizare adecvată este definită ca
Atenuarea a = 1 nep corespunde unei scăderi a amplitudinii sau valorii efective a tensiunii sau curentului în e = 2,718 de ori.
În domeniul ingineriei radio este adesea mai ușor să se măsoare puterea semnalului la intrare și ieșire, în plus, în calcule este de preferat să se utilizeze nu logaritmi naturali, ci zecimale. Prin urmare, atenuarea este măsurată la albi:
Unitatea este destul de mare, deci folosiți 0.1 bel numit decibel.