Atunci când se înmulțește și se divide numere întregi, se aplică mai multe reguli. În această lecție vom examina fiecare dintre ele.
Când se înmulțește și se divide numerele întregi, trebuie să fii atenți la semnele cifrelor. Va depinde de aceia care se pronunță pentru aplicarea. De asemenea, este necesar să se studieze mai multe legi ale multiplicării și divizării. Studierea acestor reguli evită unele greșeli enervante în viitor.
Legile multiplicării
Unele legi ale matematicii considerate în lecție sunt legile matematicii. Dar nu am luat în considerare toate legile. Există multe legi în matematică și va fi mai înțelept să le studiem în mod consecvent, după cum este necesar.
Pentru început, amintiți-vă de ce se compune multiplicarea. Înmulțirea constă în trei parametri: multiplicarea. multiplicatorul și produsul. De exemplu, ia în considerare cea mai simplă expresie:
Aici 3 este un multiplicator, 2 este un multiplicator, iar 6 este un produs.
Înmulțirea arată exact ce creștem. În exemplul nostru, creștem numărul 3.
Multiplicatorul arată de câte ori este necesară creșterea multiplicării. În exemplul nostru, multiplicatorul este numărul 2. Acest multiplicator indică de câte ori să crească multiplicatorul de 3. Astfel, în timpul operației de multiplicare, numărul 3 va fi dublat.
Produsul este rezultatul real al operației de multiplicare. În exemplul nostru, produsul este numărul 6. Acest produs este rezultatul înmulțirii lui 3 cu 2.
Expresia 3 × 2 poate fi de asemenea înțeleasă ca suma a două triple. Multiplicatorul 2 în acest caz va arăta de câte ori este necesar să adăugați trei:
Legea multiplicatoare a multiplicării
Am luat deja în considerare legea deplasării multiplicării în lecția legilor matematicii. Să o repetăm din nou.
Multiplicatorul și multiplicatorul sunt numite un cuvânt comun - factorii. Legea relativă a înmulțirii este după cum urmează:
Din rearanjarea locurilor factorilor, produsul nu se schimbă.
Să verificăm dacă este așa. Se multiplică prin exemplul 3 cu 5. Aici 3 și 5 sunt factori.
Acum schimbăm factorii:
În ambele cazuri, primim răspunsul 15, apoi între expresiile 3 × 5 și 5 × 3 putem pune un semn egal, deoarece ele poartă același înțeles:
Și cu ajutorul variabilelor, legea deplasării multiplicării va arăta astfel:
unde a și b sunt factori
Legea multiplicatoare a multiplicării
Această lege spune că dacă expresia constă în mai mulți factori, atunci produsul nu va depinde de ordinea acțiunilor.
De exemplu, expresia 3 × 2 × 4 constă din mai mulți factori. Pentru ao calcula, mai întâi puteți înmulți 3 și 2, apoi multiplicați produsul rezultat cu numărul 4 rămas. Se va arăta astfel:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
Aceasta a fost prima versiune a soluției. A doua opțiune este că puteți înmulți mai întâi 2 și 4, apoi multiplicați produsul rezultat cu numărul rămas 3. Acesta va arăta astfel:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
În ambele cazuri, primim răspunsul 24. Prin urmare, putem pune un semn egal între expresii, deoarece ele poartă același înțeles:
(3 × 2) × 4 = 3 × (2 × 4)
și folosind variabilele, legea combinării de înmulțire poate fi scrisă ca:
a × b × c = (a × b) × c = a × (b × c)
unde în loc de a, b, c poate sta orice număr.
Legea distributivă a multiplicării
Această lege am studiat în lecțiile de lecție ale matematicii. Să o repetăm din nou.
Legea distributivă a multiplicării ne permite să multiplicăm suma cu un număr. Pentru a face acest lucru, fiecare termen al acestei sume este înmulțit cu acest număr, iar rezultatele obținute se adaugă.
De exemplu, găsim valoarea expresiei (2 + 3) × 5
Expresia în paranteze este suma. Această sumă trebuie să fie înmulțită cu numărul 5. Pentru aceasta, fiecare termen al acestei sume, adică numerele 2 și 3, trebuie înmulțit cu numărul 5 și se adaugă rezultatele care rezultă:
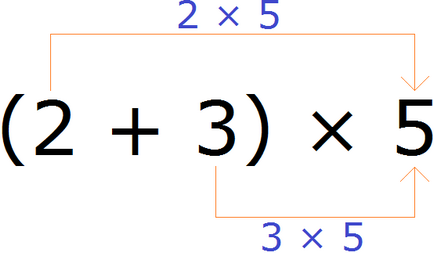
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Prin urmare, valoarea expresiei (2 + 3) × 5 este de 25.
Folosind variabilele, legea distributivă a înmulțirii este scrisă astfel:
(a + b) × c = a × c + b × c
unde în loc de a, b, c poate sta orice număr.
Legea multiplicării cu zero
Această lege spune că dacă în orice înmulțire există cel puțin un zero, atunci răspunsul este zero. Legea arată astfel:
Produsul este egal cu zero dacă cel puțin unul dintre factori este zero.
De exemplu, expresia 0 × 2 este zero
Se pune întrebarea: "De ce se întâmplă acest lucru?" În acest caz, cei doi reprezintă un multiplicator și indică de câte ori crește multiplicatorul. Asta este, de câte ori să crească zero. În mod literal, această expresie este citită ca "crește zero la jumătate". Dar cum puteți mări zero la jumătate, dacă este zero?
Cu alte cuvinte, dacă "nimic" nu este dublat sau chiar un milion de ori, va fi în continuare "nimic".
Și dacă modificați factorii în expresia 0 × 2, din nou se dovedește a fi zero. Acest lucru știm din legea anterioară de relocare:
Exemple de aplicare a legii de înmulțire cu zero:
2 × 5 × 0 × 9 × 1 = 0
În ultimele două exemple, există mai mulți factori. Văzându-le în zero, am pus imediat răspunsul la zero, folosind legea multiplicării cu zero.
Am luat în considerare legile de bază ale multiplicării. Apoi, ia în considerare multiplicarea numărului întreg.
Înmulțirea numerelor întregi
Exemplul 1. Găsiți valoarea expresiei -5 × 2
Aceasta este înmulțirea numerelor cu semne diferite. -5 este un număr negativ, iar 2 este un număr pozitiv. Pentru astfel de cazuri, trebuie aplicată următoarea regulă:
Pentru a multiplica numerele cu semne diferite, trebuie să le multiplicați modulele și să puneți un semn minus înainte de răspuns.
-5 × 2 = - (| -5 | × | 2 |) = - (5 × 2) = - (10) = -10
În general scrieți mai scurtă: -5 × 2 = -10
Se pune întrebarea "de ce se întâmplă acest lucru?" Faptul este că orice multiplicare poate fi reprezentată ca o sumă de numere. De exemplu, ia în considerare expresia 2 × 3. Este 6.
Multiplicatorul din această expresie este numărul 3. Acest multiplicator indică de câte ori să măriți suma. Dar expresia 2 × 3 poate fi de asemenea reprezentată ca o sumă de trei două:
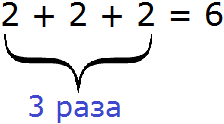
Același lucru se întâmplă și cu expresia -5 × 2. Această expresie poate fi reprezentată ca sumă
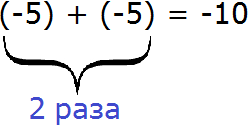
Și expresia (-5) + (-5) este -10 și o știm din ultima lecție. Aceasta este adăugarea de numere negative. Rețineți că rezultatul adăugării de numere negative este un număr negativ.
Exemplul 2. Găsiți valoarea expresiei 12 × (-5)
Aceasta este înmulțirea numerelor cu semne diferite. 12 este un număr pozitiv, (-5) este un număr negativ. Din nou, aplicați regula anterioară. Înmulțiți modulele numerice și puneți un semn minus înainte de răspuns:
12 × (-5) = - (| 12 | s | -5 |) = - (12 × 5) = - (60)
De obicei scrise mai scurte: 12 × (-5) = -60
Exemplul 3. Gasiti valoarea expresiei 10 × (-4) × 2
Această expresie constă în mai mulți factori. Mai întâi, multiplicați 10 și (-4), apoi multiplicați rezultatul cu 2. În trecere, aplicăm regulile învățate anterior:
10 × (-4) = - (| 10 | × | -4 |) = - (10 × 4) = (-40) = -40
-40 × 2 = - (| -40 | × | 2 |) = - (40 × 2) = - (80) = -80
Prin urmare, valoarea expresiei 10 × (-4) × 2 este de -80
De obicei scrise mai scurte: 10 × (-4) × 2 = -40 × 2 = -80
Exemplul 4. Găsiți valoarea expresiei (-4) × (-2)
Aceasta este multiplicarea numerelor negative. În astfel de cazuri, trebuie aplicată următoarea regulă:
Pentru a multiplica numerele negative, trebuie să le multiplicați modulele și să introduceți un semn plus înainte de răspuns
(-4) × (-2) = | × | -2 | = 4 × 2 = 8
În plus, prin tradiție, nu scriem, așa că am notat doar răspunsul 8.
În general, scrieți o scurtă (-4) × (-2) = 8
Se pune întrebarea: atunci când se multiplică numerele negative, apare brusc un număr pozitiv. Să încercăm să dovedim că (-4) × (-2) este 8 și nimic altceva.
Mai întâi, scrieți următoarea expresie:
Puneți-l în paranteze:
Adăugați la expresie expresia noastră (-4) × (-2). De asemenea, l-am pus în paranteze:
Toate acestea sunt egale cu zero:
Acum începe distracția. Linia de fund este că trebuie să calculăm partea stângă a acestei expresii și, ca rezultat, să obținem 0.
Astfel, primul produs (4 × (-2)) este -8. În această expresie, scriem numărul -8 în locul produsului (4 × (-2))
Acum, în locul celui de-al doilea produs, am pus temporar elipsa
Acum uita-te atent la expresia -8 + [...] = 0. Ce număr ar trebui să fie în locul unei elipse, astfel încât să se respecte egalitatea? Răspunsul se sugerează. În loc de elipsă trebuie să existe un număr pozitiv de 8 și nu altul. Numai în acest fel va fi respectată egalitatea. La urma urmei, -8 + 8 este 0.
Vom reveni la expresia -8 + ((-4) × (-2)) = 0 și vom înlocui produsul ((-4) × (-2)) cu numărul 8
Exemplul 5. Găsiți valoarea expresiei -2 × (6 + 4)
Aplicăm legea distributivă a multiplicării, adică multiplicăm numărul -2 cu fiecare suma sumă (6 + 4)
-2 × (6 + 4) = (-2 × 6) + (-2 × 4)
Acum calculați expresiile în paranteze. Apoi combinăm rezultatele. În paralel, aplicăm regulile învățate anterior. Înregistrarea cu module poate fi omisă, pentru a nu deranja expresia
-2 × 6 = - (2 × 6) = - (12) = -12
-2 × 4 = - (2 × 4) = - (8) = -8
Prin urmare, valoarea expresiei -2 × (6 + 4) este -20
În general scrieți mai scurtă: -2 × (6 + 4) = (-12) + (-8) = -20
Exemplul 6. Găsiți valoarea expresiei (-2) × (-3) × (-4)
Expresia constă în mai mulți factori. Mai întâi, multiplicați numerele -2 și -3 și multiplicați produsul rezultat cu numărul rămas -4. Trecem peste înregistrare cu modulele, astfel încât să nu aglomera expresia
Prin urmare, valoarea expresiei (-2) × (-3) × (-4) este -24
De obicei scrieți mai scurtă: (-2) × (-3) × (-4) = 6 × (-4) = -24
Legile diviziunii
Înainte de împărțirea întregului număr, este necesar să studiem două legi divizionare.
Mai întâi de toate, să ne amintim de ce se compune diviziunea. Diviziunea constă din trei parametri: un dividend. divizorul și coeficientul. De exemplu, ia în considerare cea mai simplă expresie:
Aici 8 este un dividend, 2 este un divizor, 4 este un coeficient.
Divizibilul arată exact ce împărțim. În exemplul nostru, împărțim numărul 8.
Divizorul arată câte părți au divizat dividendul. În exemplul nostru, divizorul este numărul 2. Acest divizor arată câte părți au divizat dividendul 8. Aceasta înseamnă că, în timpul operațiunii de divizare, numărul 8 va fi împărțit în două părți.
Privat - acesta este, de fapt, rezultatul operațiunii divizării. În exemplul nostru, coeficientul este numărul 4. Acest coeficient este rezultatul împărțirii între 8 și 2.
Apoi, ia în considerare legile diviziunii.
Nu puteți să vă împărțiți cu zero
Orice număr este interzis să se împartă cu zero. Întrebarea este "de ce?".
Faptul este că diviziunea este operația inversă a multiplicării. De exemplu, dacă 2 × 6 = 12, atunci 12 = 6
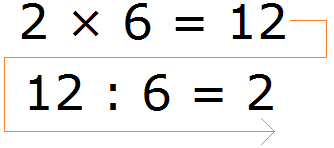
Se poate observa că a doua expresie este scrisă în ordine inversă.
Acum facem același lucru pentru expresia 5 × 0. Știm din legile de multiplicare că produsul este zero dacă cel puțin unul dintre factori este zero. Prin urmare, expresia 5 × 0 este zero
Dacă scriem această expresie în ordine inversă, obținem:
Imediat, răspunsul este 5, care se obține ca rezultat al împărțirii zero la zero. Acest lucru este imposibil și stupid.
În ordinea inversă, puteți scrie o altă expresie similară, de exemplu 2 × 0 = 0
În primul caz, împărțind zero la zero, avem 5, iar în cel de-al doilea caz 2. Asta este, de fiecare dată când împărțim zero la zero, putem obține valori diferite și acest lucru este inadmisibil în matematică.
Aceasta a fost prima explicație a motivului pentru care nu puteți diviza la zero.
A doua explicație este că împărțirea unui dividend de către un divizor înseamnă găsirea unui număr care, înmulțit cu un divizor, va da un dividend.
De exemplu, expresia 8. 2 înseamnă a găsi un număr care, înmulțit cu 2, dă 8
Aici, în loc de elipsă, trebuie să existe un număr care, înmulțit cu 2, dă răspunsul 8. Pentru a găsi acest număr, este suficient să scrieți această expresie în ordine inversă:
Acum, să ne imaginăm că trebuie să găsim valoarea expresiei 5. 0. În acest caz, 5 este un dividend și 0 este un divizor. Împărțiți 5 cu 0 înseamnă să găsiți un număr care, înmulțit cu 0, dă 5
Aici, în loc de elipsă, trebuie să existe un număr care, înmulțit cu 0, dă un răspuns de 5. Dar nu există un număr care, înmulțit cu zero, dă 5.
Expresia [...] × 0 = 5 contrazice legea multiplicării cu zero, care prevede că produsul este zero când cel puțin unul dintre factori este zero.
Deci, pentru a scrie expresia [...] × 0 = 5 în ordine inversă, împărțirea lui 5 la 0 nu are sens. Prin urmare, ei spun că nu poți să divizi cu zero.
Folosind variabilele, această lege este scrisă după cum urmează:
Această expresie poate fi citită după cum urmează:
Numărul a poate fi împărțit la numărul b. cu condiția ca b să nu fie zero.
Această lege spune că, dacă dividendul și divizorul se înmulțesc sau se împart cu același număr, atunci coeficientul nu se va schimba.
De exemplu, luați în considerare expresia 12. 4. Valoarea acestei expresii este 3
Să încercăm să înmulțim dividendul și divizorul cu același număr, de exemplu, cu numărul 4. Dacă credem că avem proprietatea cuantificării, trebuie din nou să obținem numărul 3
(12 × 4). (4 × 4)
(12 × 4). (4 × 4) = 48. 16 = 3
Au primit răspunsul 3.
Acum încercăm să nu ne multiplicăm, ci să împărțim dividendul și divizorul cu numărul 4
(12. 4). (4,4)
(12. 4). (4,4) = 3,1 = 3
Au primit răspunsul 3.
Vedem că dacă dividendul și divizorul sunt multiplicate sau împărțite la același număr, atunci coeficientul nu se schimbă.
Am luat în considerare două legi divizionare. Apoi, ia în considerare împărțirea numerelor întregi.
Diviziunea numerelor întregi
Exemplul 1. Găsiți valoarea expresiei 12. (-2)
Aceasta este împărțirea numerelor cu semne diferite. 12 este un număr pozitiv, (-2) este un număr negativ. În astfel de cazuri, trebuie să împărțiți modulul divizibil într-un modul divizor și puneți un semn minus înainte de răspuns.
În general scrieți mai scurtă decât 12. (-2) = -6
Exemplul 2. Găsiți valoarea expresiei -24. 6
Aceasta este împărțirea numerelor cu semne diferite. -24 este un număr negativ, 6 este un număr pozitiv. În astfel de cazuri, din nou, trebuie să împărțiți modulul divizibil într-un modul divizor și puneți un semn minus înainte de răspuns.
În general, scrierea este mai scurtă decât -24. 6 = -4
Exemplu 3. Găsiți valoarea expresiei (-45). (-5)
Aceasta este împărțirea numerelor negative. În astfel de cazuri, trebuie să împărțiți modulul divizibil într-un modul divizor și să introduceți un semn plus înainte de răspuns.
(-45). (-5) = | -45 |. | -5 | = 45. 5 = 9
În general, scrierea este mai scurtă (-45). (-5) = 9
Exemplu 4. Găsiți valoarea expresiei (-36). (-4). (-3)
În ordinea acțiunilor. dacă expresia conține numai înmulțire sau împărțire, atunci toate acțiunile trebuie efectuate de la stânga la dreapta în ordinea în care urmează.
Împărțim (-36) cu (-4) și împărțim numărul rezultat cu (-3)
(-36). (-4) = | -36 |. | -4 | = 36. 4 = 9
În general, scrieți un termen mai scurt (-36). (-4). (-3) = 9. (-3) = -3
Îți place lecția?
Alăturați-vă noului nostru grup Vkontakte și începeți să primiți notificări despre lecții noi