Lampă permanentă - tipul de oscilații într-un mediu continuu, sub care fiecare punct al mediului efectuează o mișcare periodică cu o amplitudine constantă. în funcție de poziția sa.
Valurile permanente nu transferă energie.
În cazul oscilațiilor armonice într-un mediu unidimensional, un val în picioare este descris de o formulă.
.
unde u este perturbația la punctul x în momentul t, - Amplitudinea undei stătătoare este frecvența. k este vectorul de undă. - faza.
Valurile permanente sunt soluții ale acelorași ecuații de undă. Ele pot fi imaginate ca o suprapunere a valurilor care se propagă în direcții opuse.
Dacă există un val în picioare în mediu, există puncte ale căror amplitudine de oscilații este zero. Aceste puncte sunt numite noduri ale unui val în picioare. Punctele la care oscilațiile au o amplitudine maximă se numesc antinode.
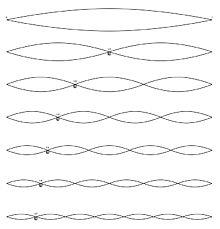
Moduri de oscilații ale unui șir
Valurile permanente apar în rezonatoare. Dimensiunile finite ale rezonatorului impun condiții suplimentare asupra existenței unor astfel de valuri. În special, pentru sistemele cu dimensiuni finite, vectorul de undă (și, prin urmare, lungimea de undă) poate lua doar anumite valori discrete. Oscilațiile cu anumite valori ale vectorului de undă sunt numite moduri.
De exemplu, diferite moduri de vibrații fixate la capetele unui șir determină tonul său fundamental și tonurile de ton.
2. Descrierea matematică a undelor în picioare
Într-un caz unidimensional, două valuri de aceeași frecvență, lungime de undă și amplitudine care se propagă în direcții opuse (opuse una față de cealaltă) vor interacționa, rezultând un val în picioare. De exemplu, o undă armonioasă propagând spre dreapta, ajungând la capătul șirului, produce un val în picioare. O undă reflectată de la capăt ar trebui să aibă aceeași amplitudine și frecvență ca valul incident.
Luați în considerare incidentul și undele reflectate sub forma:
- y 0 este amplitudinea undei,
- - Frecvența ciclică (unghiulară), măsurată în radiani pe secundă,
- k este vectorul de undă, măsurat în radiani pe metru și împărțit la lungimea de undă,
- x și t sunt variabile pentru a indica lungimea și timpul.
Prin urmare, ecuația rezultată pentru valul stator y va fi o sumă de y 1 și y 2:
Folosind relațiile trigonometrice, această ecuație poate fi rescrisă ca:
Dacă luăm în considerare modurile și antimodele. Această distanță între modurile susudnymy / antimod va fi egală cu jumătate din lungimea de undă.
3. Ecuația valurilor
Pentru a obține valuri în picioare, ca rezultat al rezolvării ecuației omogene a undelor diferențiale (d'Alembert)
este necesar să se stabilească în mod corespunzător condițiile sale limită (de exemplu, să se fixeze capetele șirului).
În cazul general al unei ecuații diferențiale neomogene
.
unde joacă rolul de "forță", prin intermediul căruia un șir este deplasat într-un anumit punct, un val stator se ridică automat.