(Notă: utilizați rezultatele obținute la paginile 31-33).
Astfel de numere raționale p q. care nu pot fi reprezentate în
forma de zecimale finite, sunt descompuse în zecimale infinite printr-o diviziune ordinară "lungă". În fiecare etapă a acestui proces apare un rest care nu este egal cu zero, altfel fracțiunea ar fi finită. Diferitele reziduuri rezultate pot fi numere întregi de la 1 la q - 1, deci există doar q - 1 posibilități pentru valorile acestor reziduuri. Aceasta înseamnă că după diviziuni q, o parte din k apare a doua oară. Dar toate celelalte rămase vor fi repetate în aceeași ordine în care au apărut deja după prima apariție a restului k. În acest fel,
descompunerea zecimală a fiecărui număr rațional are proprietatea periodicității; după un anumit număr de zecimale, același grup de zecimale începe să repete un număr infinit de ori. De exemplu, 16 = 0,16666666666. ; 1 7 = 0,142857142857142857. ;
11 1 = 0,09090909. ; 1100 122 = 0,1109090909. ; 11 90 = 0,122222222. și așa mai departe (Notă, în legătură cu acele numere raționale care sunt reprezentate
ca o zecimală finită, că această fracțiune finală poate fi imaginat, după ultima zecimală repetând la nesfârșit cifra 0, și astfel, privite numere raționale nu sunt excluse din aceasta prin formularea generală de mai sus). Aceste exemple arată că unele zecimală expansiuni corespunzătoare numerelor raționale, o "coadă" periodică este precedată de un "cap" neperiodic.
În schimb, se poate demonstra că toate fracțiunile periodice sunt numere raționale. Luați în considerare, de exemplu, o fracțiune periodică infinită
Puteți scrie: p = 100 33 + 10 -3 · 2 (1 + 10 -1 + 10 -2 +.). Expresia din

§2 CUTURI NEUTILIZATE. NUMERELE IRRAȚIONALE, LIMITE 93
În cazul general, dovada este construită în același mod, dar este complicată de necesitatea introducerii mai multor notații greoaie. Considerăm o fracție periodică a formei generale
p = 0, a 1 a 2 a 3. a m b 1 b 2 b 3. b n b 1 b 2 b 3. b n.
Indicăm prin B = 0, b 1 b 2 b 3. b n partea periodică a descompunerii noastre. Atunci putem scrie
p = 0, a 1 a 2 a 3. a m + 10-m B (1 + 10 -n + 10 -2n + 10 -3n +).
Expresia în paranteze este o progresie geometrică infinită, pentru care q = 10-n. Suma acestei progresii, conform formulei (10)
punctul este de 1 - 10-n. și prin urmare
10-m; B p = 0, a 1 a 2 a 3. a m + 1 - 10-n.
Exerciții. 1) Descompuneți următoarele numere raționale în zecimale: 11 1. 13 1. 13 2. 13 3. 17 1. 17 2. și determinați perioadele de extindere.
2) Numărul 142 857 are proprietatea că atunci când este înmulțit cu 2, 3, 4, 5 sau 6, numai permutările cifrelor sunt efectuate în el. Explicați această proprietate, pe baza extinderii numărului 1 7 în zecimal.
3) Extindeți numerele din Exercițiul 1 în fracțiuni infinite cu bazele 5, 7 și 12.
4) Extindeți numărul 1 3 într-o fracțiune binară.
5) Scrieți descompunerea 0.11212121. Setați numărul pe care îl reprezintă la baza 3 sau 5.
5. Definiția generală a numerelor iraționale prin segmente contractante. La pagina 82 am introdus o definiție preliminară: "numărul" este o fracție zecimală finită sau infinită. Cu toate acestea, am fost de acord că zecimalele, care nu reprezintă un număr rațional, sunt numite numere iraționale. Pe baza rezultatelor obținute în paragraful anterior, putem oferi acum următoarea formulare: „un continuum numeric, sau sistemul de numere reale (“ reale „numere sunt în contrast aici“ imaginar „sau“ complex“, a se vedea § 5.), este o colecție de tot felul de nesfârșită fracții zecimale ". (Atribuirea de zerouri,
SISTEMUL NUMERIC MATEMATIC
este posibil, după cum sa menționat deja, să scrieți o fracție zecimală finită
sub forma unei interminabile, sau există o altă cale: ultima cifră a unei fracții se înlocuiește cu un - 1 și să-l nenumărate îi atribuie nouari. Deci, am văzut, de exemplu, că 0.999. = 1, a se vedea punctul 3.)
Numerele rationale sunt fractiuni periodice; numerele iraționale sunt fracțiuni neperiodice. Dar o astfel de definiție nu este în întregime satisfăcătoare: într-adevăr, am văzut în capitolul I că însăși natura lucrurilor nu distinge sistemul zecimal de celelalte posibile; în același mod ar fi posibil să funcționeze, de exemplu, un sistem binar. Din acest motiv, este foarte de dorit să se definească o definiție mai generală a unui continuum numeric, independent de alegerea specială a bazei 10 sau a oricărei alte. Probabil cea mai simplă metodă pentru introducerea unei astfel de generalizări este
Considerăm pe axa numerică o secvență I 1. I 2. I 3. I n. segmente cu capete raționale; Să presupunem că fiecare segment succesiv este conținut în cel precedent și că lungimea segmentului n nn tinde la zero pentru o creștere neîngrădită a n. Vom numi o astfel de secvență de segmente "imbricate" fiecare secvență de segmente contractante. În cazul segmentelor zecimale, lungimea I n este 10-n. dar cu același succes ar putea fi, de exemplu, 2-n. sau vă puteți limita la cel puțin
de cerința ca aceasta să fie mai mică de n 1. Acum dăm următoarele
formularea care va fi considerată ca postulatul geometrică de bază, indiferent de secvență de contractare de segmente, există unul și numai un punct al axei reale, care este, de asemenea, prezentă în toate segmentele. (Este clar că nu există mai mult de un astfel de punct, deoarece lungimile segmentelor tind la zero, iar cele două puncte de vedere diferite, nu pot fi conținute într-un interval a cărui lungime va fi mai mică decât distanța dintre punctele.) Acest punct este, prin definiție, și se numește un număr real; dacă nu este rațional, atunci se numește un număr irațional. Prin această definiție, stabilim o corespondență completă între puncte și numere. Nimic fundamental nou nu a fost adăugat aici: doar definiția numărului unei fracții zecimale infinite este dată unei forme mai generale.
Cu toate acestea, cititorul în acest moment poate îmbrățișa anumite îndoieli, care ar trebui recunoscute ca pe deplin justificate. Ceea ce de fapt este că „punct“ de pe axa reală, pe care presupunem este conținută simultan în toate segmentele secvenței contractante în cazul în care nu corespunde unui număr rațional? Răspunsul nostru este: existența pe axa numerică
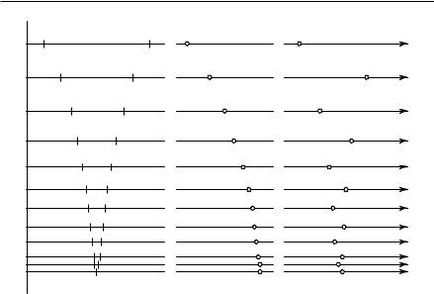
§2 CUTURI NEUTILIZATE. NUMERELE IRRAȚIONALE, LIMITE 95
Fig. 11. Întinderea segmentelor. Limite de secvență
(considerată ca o imagine geometrică) a punctului conținut în toate segmentele contractibile cu capete raționale este postulatul geometric de bază. Nu este nevoie să se reducă, ceea ce duce la alte propuneri matematice. Noi l ia acceptat ca în matematică alte axiome sau postulate, bazat pe plauzibilitate intuitiv și utilitatea sa, a găsit atunci când construirea unui sistem coerent de propuneri matematice. Puțin formal, am putea porni de la o linie dreaptă numerică, pe care o considerăm drept o colecție de puncte raționale, și apoi definim un punct irațional ca
un simbol care denotă o secvență de segmente contractante. Punctul irațional este determinat în totalitate de secvența de contractare a segmentelor raționale ale căror lungimi tind să fie zero. Prin urmare, postulatul nostru de bază este de fapt capabil să servească drept definiție. Acceptați o astfel de definiție, după ce au fost reduse la o secvență de segmente contractante sens intuitiv, afirmând că „existența“ punctul irațional - apoi abandonați „cârje intuiție“, invocată de raționamentul nostru, și dau seama că toate proprietățile matematice ale punctelor iraționale pot fi înțelese și sunt reprezentate ca proprietăți ale secvențelor de segmente contractante.
Din punct de vedere pur matematic, în acest caz, este important ca, după ce am acceptat definiția unui număr irațional ca