Având în vedere circuitul de curent continuu, este logic că, în orice punct al lanțului nu poate fi un proces de acumulare de sarcină, în caz contrar ar putea provoca o schimbare în potențiale puncte care ar determina schimbarea de tensiune în zonele de circuit electric de curent continuu. Din cele de mai sus se poate concluziona că sarcina electrică, care este potrivit pentru nodul pe unitate de timp a uneia sucursale o parte din atașată la un nod, este egal cu sarcina electrica se extinde de la nodul de pe cealaltă parte a ramurilor pentru aceeași unitate de timp. Această poziție este exprimată prin legea primului Kirchhoff și formulat după cum urmează: o sumă aritmetică a curenților care corespund unui nod este egală cu suma aritmetică a curenților de ieșire al nodului.
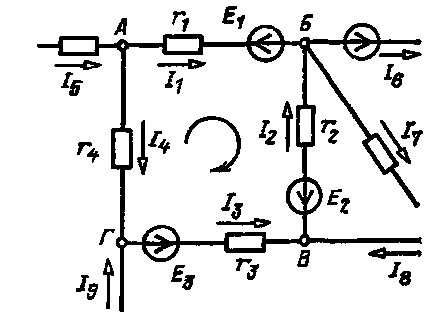
Fig.1 - O parte a circuitului electric
Folosind această lege, ca exemplu, scriem pentru nodurile A și B (figura 1) următoarele
adică prima lege Kirchhoff poate fi formulată într-un alt mod: suma algebrică a curenților la nod este zero. În acest caz, curenții care abordează nodul sunt primiți cu un semn "-", iar curenții de la nod (sau invers) sunt primiți cu un semn "+".
Când direcția curentului nu este specificată sau nu este cunoscută, atunci pentru a face ecuațiile în conformitate cu legile lui Kirchhoff. Este necesar să specificați direcțiile ramurilor actuale în ordine aleatorie și să le desemnați în circuitul electric. Curenții selectați în mod arbitrar nu reflectă distribuția corectă a curentului în circuitul electric, sunt necesari numai pentru calcul, după care vor fi elucidate direcțiile corecte ale curenților din ramificații. Direcția corectă a curentului în ramură este foarte simplă. De obicei, înainte de calcul, curenții din circuit nu sunt cunoscuți de noi, prin urmare, alegerea arbitrară a direcțiilor de curenți înseamnă că valorile curente au un semn pozitiv. Dacă, ca urmare a calculelor, orice curent are o valoare negativă, acest lucru indică faptul că direcția nu a fost aleasă corect și este necesar să se schimbe în sens invers.
Pentru a formula cea de-a doua lege a lui Kirchhoff, să aruncăm o privire mai atentă la circuitul electric prezentat în Fig. dat samavolnic circuitului de by-pass, de exemplu, sensul acelor de ceasornic, așa cum se arată în figurile 1 și uita-te la modul în care schimbările potențiale din circuit. Mai întâi, vom selecta punctul de pornire al bypass-ului, în cazul nostru este punctul A, și vom echivala potențialul acestui punct la zero (ne bazăm acest punct). Pe un site un circuit electric între punctul A și punctul B, potențialul punctului A descrește pe rezistorul r 1 prin cantitatea de cădere r circuitul 1 I 1 tensiune, deoarece direcția parcurgeri coincide cu direcția curentului (deoarece fluxurile curente din înalt punct potențial la un punct potențial inferior). În plus, potențialul continuă să scadă, în aceeași secțiune, de magnitudinea EMF E1 (săgeata sursă a EMF indică un terminal pozitiv). prin urmare
Pe parcursul tranziției de la punctul B la punctul B, potențialul este mărit cu r cădere de tensiune de 2 I 2 (deoarece ocolesc circuitul în această regiune împotriva curentului I 2), iar cantitatea de CEM E2 (așa cum vom trece de la borna negativă la polul pozitiv, altele în cuvinte, de la un potențial mai mic la unul mai mare).
Mergem în jurul întregului contur, revenind la punctul A, obținem ecuații
Noi purtăm picături de tensiune pe elementele pasive în partea dreaptă a ecuației
Această expresie este legea a doua a lui Kirchoff, și se pare că: suma algebrică a EMF într-un circuit închis, este egală cu suma algebrică a căderilor de tensiune în rezistențe. În formularea ecuațiilor conform celei de-a doua legi a lui Kirchhoff. trebuie luat în considerare faptul că EMF este luat cu un semn "+", în cazul în care direcția EMF coincide cu direcția de by-pass de circuit, în caz contrar EMF este luat cu un semn "-". Mărimea căderii de tensiune pe rezistență este luată cu semnul "+" dacă direcția curentă coincide cu direcția de by-pass de circuit și invers.