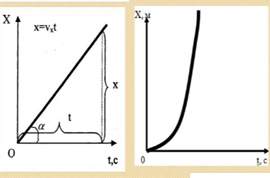
În acest articol vom vorbi despre mișcare, sau mai degrabă despre unele forme. În primul rând, vom analiza mișcarea însăși, care poate fi descrisă ca o schimbare a poziției unui obiect în spațiul unui alt obiect relativ. Mișcarea mecanică este împărțită în trei tipuri:
- Mișcarea unui punct solid.
- Propunerea de mediu continuu.
- Mișcarea unui corp rigid.
Tipuri de obiecte supuse mișcării
Materialele corpului includ corpuri care au o masă, însă structura, forma, mărimea și forma lor pot fi neglijate pentru a simplifica rezolvarea acestei probleme. Mișcarea depinde numai de schimbarea coordonatelor în timp, ceea ce este indicat de viteză. Mișcarea unui punct poate fi curbila atunci când se deplasează de-a lungul oricărei traiectorii și rectilinie, când viteza mișcării nu se abate de la linia dreaptă și direcția sa rămâne neschimbată pe toată durata călătoriei.
Dacă numărul de puncte nu este limitat, ci sunt unite de condiția continuității câmpurilor de viteză, astfel de mișcări pot descrie schimbările în poziția lichidelor și a substanțelor gazoase în spațiu și se numesc mișcări de medii continue. Punctele se pot mișca independent unul de celălalt, limitându-se la limitele materiei.
Dacă caracteristicile obiectului nu pot fi neglijate, atunci acesta este un corp solid care are, pe lângă masă, și o formă, o structură (cristalină și amorfă), o stare agregată (în acest caz o stare solidă). Mișcarea sa reprezintă un sistem de calcul ceva mai diferit - constă în viteza oricărui punct al obiectului și mișcarea de rotire în jurul acestui punct.
Mișcare uniformă
Mișcarea uniformă există atunci când viteza obiectului rămâne aceeași la orice interval al traseului parcurs. În acest caz, timpul de trecere a oricăror două secțiuni identice va fi același.
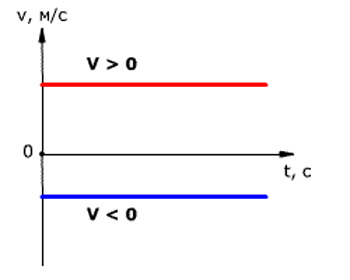
Acest tip de mișcare poate fi de două tipuri:
- Într-o linie dreaptă, atunci când vectorul de viteză nu se schimbă.
- Pe un cerc, atunci când un vector se schimbă, acest tip este de asemenea referit ca fiind la fel de accelerat, deoarece vectorul se schimbă în mod constant.

Miscarea la fel de accelerata
Miscarea la fel de accelerata nu are aceeasi viteza pe intreaga cale. În acest caz, există o accelerație, care este responsabilă pentru o creștere constantă a vitezei. Accelerația în această formă de mișcare rămâne neschimbată, iar viteza crește constant și uniform. Teoretic la infinit. dacă obiectul se mișcă în raport cu un alt obiect, la viteza unei viteze reduse a luminii, dacă viteza sa este considerată relativă la obiectul în sine.
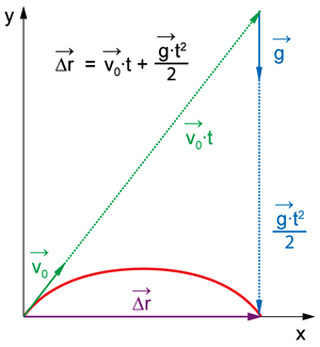
Dacă în calcule sunt incluse alte proprietăți, viteza finală va fi chiar mai mică. Pe lângă accelerarea la fel de rapidă, există și o mișcare la fel de înceată, unde modulul vitezei scade uniform. De asemenea, mișcarea uniform accelerată poate apărea în mai multe dimensiuni, în legătură cu care se întâmplă:
În cazul primei, mișcarea este de-a lungul unei axe de coordonate. În cazul celui de-al doilea, pot fi adăugate alte măsurători.

Diferența dintre cele două tipuri de mișcări
Mișcarea uniform accelerată diferă de mișcarea uniformă prin faptul că viteza în această mișcare crește constant și crește uniform. până la o anumită limită. Cu toate acestea, într-o mișcare uniformă, viteza nu se schimbă, altfel această mișcare nu se va numi uniformă. În mod similar, în mișcarea uniformă, modificările vitezei și timpului de trecere a unei anumite secțiuni a spațiului sunt imposibile. Un exemplu de mișcare accelerată uniform poate fi un obiect aruncat sub un unghi la orizont, cu condiția să existe un câmp uniform de gravitate.
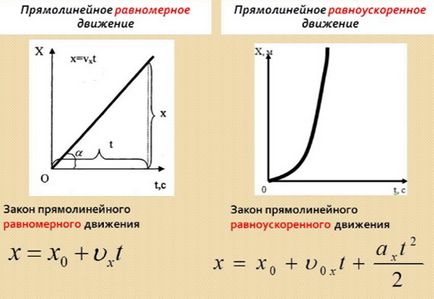
În determinarea unuia și a celuilalt tip de mișcare este importantă nu numai modificarea accelerației, ci și schimbarea vectorului său, care nu poate coincide cu vectorul de viteză. Dacă vectorul de accelerație se modifică și accelerația însăși nu este prezentă, atunci aceste mișcări pot fi simultan accelerate și uniformizate uniform. O astfel de mișcare este o mișcare de-a lungul unui cerc într-un spațiu plat bidimensional.
aplicații
Formulele pentru astfel de mișcări pot fi aplicate în planuri complet diferite. De exemplu, pentru a calcula căderea solidelor în cădere liberă, pentru a prezice punctul de incidență. De asemenea, pentru o varietate de calcule matematice și geometrice.