Prin definiție, funcția de transfer (PF) este un operator egal cu raportul dintre imaginea de ieșire și coordonatele de intrare în condiții inițiale zero:
Scopul serviciului. Obiectul de control (OA) este descris printr-o ecuație diferențială liniară de ordin n. Pentru o legătură oscilantă a ordinului n, se determină următoarele:- funcția de transfer;
- caracteristici de frecvență (amplitudine (AFC), fază (PFC), logaritmică (LPC));
- funcții tranzitorii și impulsive (greutate);
- grafice ale caracteristicilor tranzitorii și de frecvență.
Pentru a găsi funcția de transfer online, trebuie să selectați
Un exemplu. Obiectul de control (OA) este descris printr-o ecuație liniară diferențială a ordinii a treia:
(2)
1) Funcția de transfer a op amperi în cazul general poate fi reprezentată ca un raport
W (# 969;) = A (# 969;) e i # 966; (# 969;) =
unde R (p) și Q (p) sunt imagini Laplace ale variabilelor de ieșire și de intrare ale OU corespunzătoare părților stângi și drepte ale ecuației 1. Prin urmare, funcția de transfer va avea forma:
(3)
sau
. (4)
2) Definiți caracteristicile de frecvență ale amplificatorului op. Se știe că funcția de transfer de frecvență W (# 969;) poate fi reprezentată ca:
, (5)
unde răspunsul A (# 969;) - frecvența de amplitudine (AFC);
# 966; (# 969;) - răspunsul la frecvența fazei (PFC);
U (# 969;) - răspuns real în frecvență (VCHH);
V (# 969;) - răspunsul imaginar al frecvenței;
Înlocuim i # 969; în expresia (3) în loc de p. Avem:
(6)
Pe baza expresiilor (5) și (6), izolați separat caracteristicile de frecvență și amplitudine și înlocuim valorile numerice ale coeficienților. Deoarece:
A (# 969;) = | W (i # 969;)
# 966; (# 969;) = arg (W (i # 969;))
(vedeți numere complexe). În cele din urmă obținem: (7)
3) Definiți răspunsul frecvenței de amplitudine logaritmică (LATCH).
Se știe că LACHH este determinat din relația:
L (# 969;) = 20 lg (A (# 969;)) (8)
Această caracteristică are dimensiunea dB (decibeli) și arată schimbarea raportului puterii de ieșire cu puterea de intrare. Pentru confort, LATCH este construit pe o scară logaritmică.
Caracteristica de fază a fazei, construită pe o scară logaritmică, va fi numită răspunsul de frecvență fazei logaritmice (LPCF).
Exemple de construcție a LAPH și LPCh pentru datele noastre inițiale sunt prezentate în figura 1.
Să determinăm funcția tranzitorie (greutate) impulsivă. Funcția de greutate w (t) este răspunsul sistemului la funcția de impuls a unității aplicată intrării sale. Funcția de greutate este legată de funcția de transfer prin transformarea Laplace.
. (9)
În consecință, funcția de greutate poate fi găsită prin aplicarea transformării inverse Laplace la funcția de transfer.
w (t) = L-1 [W (p)] (10)
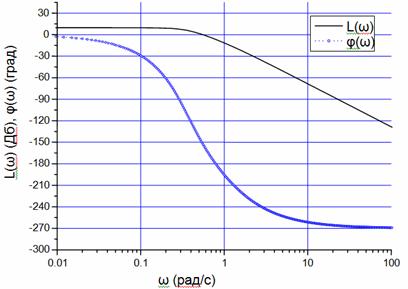
Figura 1 - Sistem L (# 969;) - LACH (dB); # 966; (# 969;) - LPCh a sistemului (grad); # 969; - frecvența semnalului de intrare (rad / s)
Să calculam aproximativ rădăcinile polinomilor R (p) și Q (p). și apoi găsim transformarea inversă Laplace din funcția de transfer și construim graficul funcției de greutate (Figura 2). Funcția de greutate este un derivat al funcției de tranziție h (t). care este răspunsul sistemului la o acțiune pas cu pas. Integrarea w (t) sau efectuarea transformării inverse Laplace peste W (p) / p. găsim funcția de tranziție h (t) și construim graficul corespunzător (figura 3).
,
.
Figura 2 - Caracteristicile de timp. Funcția de răspuns impuls w (t)
Figura 3 - Funcția de tranziție h (t)