Cu încărcare verticală în grosimea solului care nu este lut, apar zone de forfecare. În bazinele de pământ și bazele lor, aceste zone formează împreună suprafețele de forfecare. Dacă forțele reactive pe suprafața de forfecare sunt mai mici decât forțele exterioare, structura pierde stabilitate. Pierderea stabilității este însoțită de deformări inacceptabile, în urma cărora structura se descompune.
Natura deformațiilor în funcție de sarcina externă poate fi urmărită în conformitate cu graficul prezentat în figura 11.
Studiile au demonstrat că solul sub presiune exercitat de o forță externă suferă ulterior trei etape de deformare.
Prima etapă (pe linia grafică OM1) se caracterizează printr-o relație liniară între sarcină și deformare. Aici există numai compactarea solului
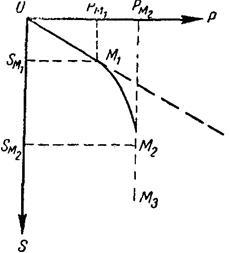
Fig. 11 Etapele de deformare a tensiunii:
p - sarcină externă; S este deformarea solului.
datorită deplasării verticale a particulelor solide și, ca o consecință, unei scăderi a porozității. O astfel de deformare este considerată admisibilă și conduce la scufundarea de tiraj, care este calculată prin calcul.
A doua etapă (pe curba curbei M1 M2) este caracterizată prin prezența zonelor de forfecare datorită deplasării orizontale a particulelor, în timp ce mișcările verticale în această etapă au o valoare neglijabilă. Deformarea liniară dispare aici. Creșterea tensiunii crește mai repede decât sarcina.
A treia etapă (pe linia M2 M3) corespunde izbucnirii solului, iar deformarea are loc brusc și are consecințe catastrofale.
Este absolut evident că orice structură construită pe o bază non-bazică, să nu mai vorbim de un baraj de pământ, poate funcționa în mod normal numai în prima etapă, când solul este compactat.
Parametrii care determină stabilitatea barajului în prima etapă a deformării sunt frecarea internă și coeziunea solului.
Fricțiunea internă în sol creează o forță reactivă definită de formula:
unde T este forța internă de frecare;
N este componenta normală a sarcinii externe;
- unghiul de frecare internă.
Forța T este caracteristică solurilor libere (nelegate) și este compusă din:
a) rezistența la frecare atunci când se deplasează o particulă peste alta;
b) rezistența la rularea unor particule față de altele;
c) rezistența la fragmentarea particulelor și unghiurile de așchiere.
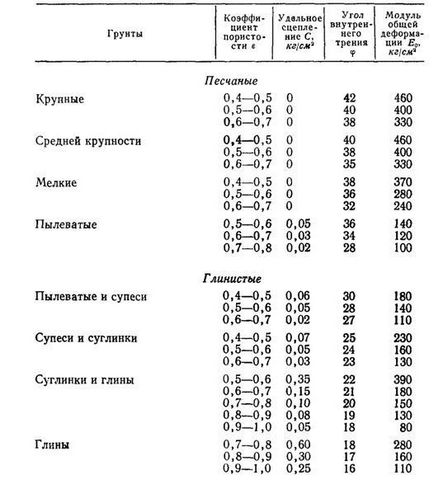
Valorile calculate ale unghiurilor interne de frecare pentru solurile libere (nelegate) și argile (coezive), în funcție de coeficientul de porozitate, sunt prezentate în Tabelul 12.
Forțele coezive se manifestă în soluri coezive și se datorează prezenței cimenturilor naturale (geluri și săruri coloidale), fenomenelor moleculare și presiunii capilare. De asemenea, aderența este afectată de umiditate, iar cu creșterea acesteia, ambreiajul scade.
Forța reactivă în solurile coezive este determinată de formula:
Din punct de vedere grafic, dependența (23) poate fi reprezentată ca o linie dreaptă cu o înclinare față de axa abscisă, cu o ordonată inițială egală cu C (figura 12). unghi
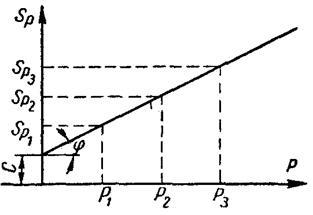
Fig. 12. Relația dintre presiunea normală și forța de forfecare (pentru solurile argiloase)
Panta liniei drepte este determinată de unghiul de frecare internă.
Valorile aproximative calculate ale coeziunii specifice pentru solurile coezive sunt prezentate în Tabelul 12.