Proprietățile cuantice ale radiației electromagnetice 1. Radiația termică și luminiscența
Radiația termică și luminiscența. Caracteristicile spectrale ale radiației termice
Radiația termică este emanația undelor electromagnetice datorită energiei interne a corpurilor. Radiația termică are loc la orice temperatură. La temperaturi scăzute, acesta este mutat la partea cu unde lungi a spectrului.
Radiația va fi echilibrată dacă distribuția de energie între corp și radiație nu se va schimba pentru fiecare lungime de undă. Capacitatea radiației termice de a fi în echilibru se datorează faptului că intensitatea acestei radiații crește cu temperatura.
Fluxul de energie emis de suprafața unitară a corpului radiant în toate direcțiile (în unghiul solid 2π) se numește luminozitatea energetică a corpului R. Luminozitatea energiei este o funcție a temperaturii.
Radiația include valuri de frecvențe diferite # 969; (lungime de undă # 955; ). Fie ca fluxul de energie emis de suprafața unității corpului în intervalul de frecvență d # 969 să fie egal cu. De aceea, valoarea este mică
o cantitate se numește emisivitatea corpului. Aceasta este puterea de radiație pe unitatea de suprafață a suprafeței corpului în intervalul de frecvență al lățimii unității. Emisivitatea este o funcție a frecvenței radiației și a temperaturii.
Luminozitatea energetică a unui corp este legată de emisivitatea sa prin formula
Radiația poate fi caracterizată în loc de frecvența lungimii de undă. Intervalul spectral corespunde intervalului de lungime de undă. și. Apoi, diferențiând, obținem
Semnul minus din această expresie nu este semnificativ, arată doar că, odată cu mărirea lungimii de undă, scade. Prin urmare, nu vom scrie un minus în viitor.
Fracția luminozității energetice pe interval este
Deoarece intervalele aparțin aceleiași secțiuni a spectrului, cantitățile u trebuie să coincidă, adică , sau
cu ajutorul formulei (1.2) este posibil să trecem de la k și invers.
Toate corpurile absorb o anumită măsură energia undei electromagnetice. Caracteristica spectrală a absorbției este absorbția corpului (coeficientul de absorbție monocromatică)
d # 969; - un curent de energie electromagnetică care intră pe corp, dF # 969; - partea din fluxul absorbit de corp este o funcție a frecvenței radiației și a temperaturii acesteia (1).
Dacă corpul absoarbe complet incidentul energetic pe acesta (= 1), se numește absolut negru. Un corp a cărui capacitate de absorbție nu depinde de frecvență și la o temperatură fixă are o constantă și mai mică decât o valoare, se numește gri, adică =. = const<1.
În cazul radiației de echilibru, regula Prevost este satisfăcută: dacă două corpuri absorb cantități diferite de energie, atunci și radiațiile lor vor fi diferite. Cu cât este mai mare emisivitatea corpului. cu atât este mai mare absorbanța acestuia.
Legea lui Kirchhoff afirmă că raportul dintre abilitățile emise și absoarbe nu depinde de natura corpului, este pentru toate organismele aceeași funcție (universală) a frecvenței (lungimea de undă) și a temperaturii:
Este funcția Kirchhoff universală. Pentru un corp absolut negru = 1, deci =. astfel, există o capacitate emancipatoare a unui corp absolut negru.
În studiile teoretice, este mai convenabil să se folosească funcția de frecvență pentru a caracteriza compoziția spectrală a radiației termice de echilibru. În lucrările experimentale este preferabilă utilizarea funcției. în acest caz
Trupurile absolut negre nu există în natură. Unele corpuri sunt aproape de negru în anumite condiții. Radiația soarelui poate fi considerată aproape de emisia unui corp absolut negru. Hârtia neagră absoarbe 96% din incidentul energetic pe acesta, funinginea - 98%, catifea neagră - 99,6%. Funcția de funingine, negru de platină. aproape de 1 numai într-un interval de frecvență limitat. În regiunea infraroșie <<1.
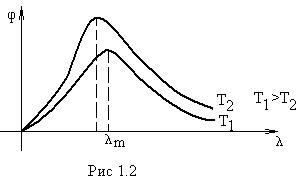
Pentru fiecare curbă există un maxim. Aceasta indică faptul că energia este distribuită inegal pe întregul spectru al unui corp absolut negru - în regiunea frecvențelor foarte mici și foarte înalte, un corp absolut negru aproape nu emite energie. Cu o creștere a temperaturii, deplasarea maximă la o regiune cu lungimi de undă mai scurte. Zonă limitată de o curbă. este proporțională cu luminozitatea energetică a lui R # 969, T la o temperatură dată și crește cu creșterea temperaturii.
Să luăm în considerare radiația care este în echilibru cu materia. Pentru a face acest lucru, imaginați-vă o cavitate izolată, pereții căruia se mențin la o temperatură constantă T. În starea de echilibru, energia radiației va fi distribuită în volumul cavității cu o anumită densitate. Distribuția spectrală a acestei energii poate fi caracterizată printr-o funcție. determinată de condiție. unde este fracțiunea densității energetice pe interval de frecvență. Densitatea totală a energiei este
Densitatea energetică de echilibru a radiației depinde doar de temperatură și nu depinde de proprietățile cavității.
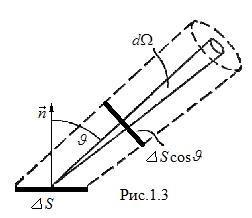
Luăm o suprafață elementară pe suprafața cavității. Această platformă trimite într-un unghi solid în direcția care formează un unghi cu cel normal. fluxul de energie.
În toate direcțiile în unghiul solid 2. platforma trimite un flux de energie
Această egalitate trebuie îndeplinită pentru fiecare componentă spectrală a radiației. atunci
1.2 Legile lui Kirchhoff, Stefan-Boltzmann și Wine. Trupul absolut negru. Formula Rayleigh-Jeans și "catastrofa ultravioletă". Ipoteza cuanților. Planul lui Planck. Explicație cuantică a legilor radiației termice
a) Legile lui Stefan-Boltzmann și ale vinului. Fundamentarea teoretică a legilor radiației unui corp absolut negru a fost de mare importanță în istoria fizicii - a dus la conceptul de quanta de energie.
Pentru a caracteriza complet radiația termică, este necesar, așa cum arată legea lui Kirchhoff, să cunoaștem forma funcției Kirchhoff f (# 969 ;, T). și anume este necesar să se stabilească forma dependenței emisivității unui corp absolut negru la temperatura sa. În 1879, Stefan, pe baza generalizării datelor experimentale, a obținut că luminozitatea energetică R a oricărui corp este proporțională cu a patra putere de temperatură. În 1884, omul de știință L. Boltzman a aplicat metoda termodinamică studiului "radiației negre" și a arătat că legea descoperită de Ștefan este aplicabilă numai pentru un corp absolut negru
Această relație a fost numită legea lui Stefan-Boltzmann. aici # 963; - constanta Stefan-Boltzmann (# 963; = 5.7 .10 W / m · K).
Legea lui Stefan-Boltzmann dă dependența luminozității energetice la temperatură.
Vin (1893) a folosit, pe lângă termodinamică, teoria electromagnetică și a arătat că funcția de distribuție spectrală ar trebui să aibă forma
unde F este o funcție a raportului dintre frecvență și temperatură. Pentru funcție, expresie
unde este o anumită funcție a produsului.
Relația (1.3) ne permite să stabilim relația dintre lungimea de undă. pe care se încadrează maximul funcției. și temperatura. Diferențăm această expresie prin:
Expresia în paranteze pătrate este o funcție. La lungimea de undă. corespunzătoare maximului funcției. Expresia (1.4) ar trebui să ajungă la zero și, din moment ce . apoi = 0. Soluția acestei ecuații conduce la relația:
care se numește legea deplasării Wien. Aici este vinul constant,
lungimea de undă corespunzătoare valorii maxime de emisivitate a unui corp absolut negru este invers proporțională cu temperatura sa. Din această lege rezultă că atunci când temperatura unui corp absolut negru este redusă, energia maximă a radiației sale se deplasează în regiunea undelor lungi. Prin urmare, atunci când temperatura este redusă, căldura albă devine roșie și apoi în infraroșu.
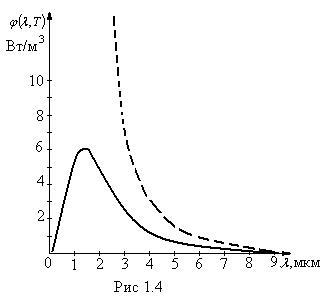
Rayleigh și Jeans în studiile lor au pornit de la teorema statisticilor clasice privind echilibrarea energiei în grade de libertate. Ei au crezut că pentru fiecare oscilație electromagnetică a oscilatorului de radiație există o energie egală cu două jumătăți ale lui kT la energia electrică, cealaltă la cea magnetică și pentru a obține următoarea formă a funcției Kirchhoff:
Această expresie se numește formula Rayleigh-Jeans. Ea este de acord cu experimentul în regiunea cu frecvență joasă a radiațiilor. În regiunea frecvențelor înalte, totuși, formula duce la o discrepanță puternică cu experimentul, cu legile lui Stefan-Boltzmann și Wien. Formula lui Rayleigh-Jeans implică creșterea frecvenței monotonice a funcției f (# 969 ;, T), dar de fapt f (# 969 ;, T) are un maxim și apoi scade (figura 1.4).
Formula Rayleigh-Jeans din regiunea de înaltă frecvență este în contradicție cu legea conservării energiei (energia radiațiilor crește nelimitat cu creșterea temperaturii). Acest rezultat a fost numit o catastrofă ultravioletă.
c) formula lui Planck. Din punct de vedere clasic, derivarea formulei Rayleigh și Jeans este perfectă. Prin urmare, divergența sa față de experiență a indicat existența unor legi care sunt incompatibile cu ideile fizicii clasice. In 1900 Max Planck a propus ca ipoteza schimbării continue în energie a sistemului, care a predominat în fizica clasică, nu pot fi aplicate oscilatoarele radiații și, în consecință, la molecule și atomi de corp radianți, pentru a face schimb de energie cu aceste oscilatoare. Potrivit lui Planck, energia oscilatorului poate lua doar anumite valori discrete egale cu un număr întreg de porțiuni elementare de energie - cuante de energie. Energia cuantică este proporțională cu frecvența radiațiilor, - este constanta lui Planck. Astfel, radiația și absorbția energiei de către corp nu este continuă, ci discretă, prin quanta. Constanta Planck ¼ = 1,054 · 10 J · s, are dimensiunea "timp temporal de energie". Această cantitate în mecanică este numită acțiune, prin urmare, uneori este numită cuantum de acțiune.
Într-o stare de echilibru, distribuția oscilațiilor de-a lungul valorilor energetice trebuie să respecte legea lui Boltzmann. Probabilitatea ca energia oscilației de frecvență să fie importantă. este
Valoarea medie a energiei oscilației
Pentru a efectua calculele, indicăm și presupunem că x poate lua o serie continuă de valori. atunci
Semnul logaritmului din această formulă este suma termenilor unei progresii geometrice infinite, cu primul termen egal cu. Întrucât numitorul este mai mic decât unitatea, progresia scade și
Înlocuind această sumă în (1.5), obținem
Dacă obținem expresia clasică Astfel, dacă energia ar putea lua o serie continuă de valori, valoarea sa medie ar fi egală cu
Densitatea energetică pe interval de frecvență
Aceasta este formula lui Planck. Ea este de acord exact cu experimentul în intervalul de frecvență de la 0 la și îndeplinește criteriul Wien.
La frecvențe joase <<1, поэтому можно считать, что . тогда - формула Планка переходит в формулу Рэлея–Джинса. Таким образом, формула Рэлея-Джинса является частным случаем формулы Планка для малых частот.
Integrarea expresiei (1.6) și rezolvarea ecuației în raport cu variabila x =. se poate obține legea deplasării Wien. Astfel, formula Planck oferă o descriere completă a radiației termice de echilibru.