Probleme care duc la integrări duble.
Problema volumului unui cilindru. Luați în considerare un corp cu o bază situată într-un plan mărginit de o suprafață și o suprafață cilindrică, a cărei generație este paralelă cu axa, iar limita servește drept ghid. Acest corp este numit cilindru (cilindru sau cilindru comun). Este necesar să se calculeze volumul cilindrului.
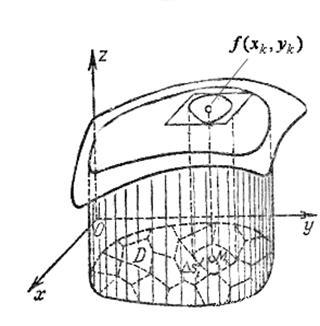
Pentru a rezolva problema, partiționăm domeniul într-un mod arbitrar în părți ale căror zone sunt de asemenea indicate prin respectiv. În fiecare dintre regiunile elementare () alegem un punct arbitrar și înmulțim valoarea funcției în acest punct cu aria domeniului. Acest produs este egal cu volumul unui corp cilindric cu suprafața de bază și înălțimea. Vom compila suma tuturor acestor produse:
Această sumă exprimă volumul unui corp cilindric în trepte care înlocuiește aproximativ un cilinderoid dat,
Indicăm diametrul regiunii elementare, adică cea mai mare distanță dintre punctele situate la limita regiunii și cea mai mare dintre aceste diametre. Evident, dacă, atunci, volumul cilindrului comun este limita de volum a corpului corespunzător al treptei cu:
Problema masei unei plăci. Să considerăm regiunea planului delimitată de o linie închisă în care se distribuie substanța cu densitate. Această regiune se numește placă. Se calculează masa plăcii prin asumarea unei funcții cunoscute.
Distribuim în mod arbitrar domeniul în regiuni ale căror zone sunt notate cu aceleași simboluri. Să presupunem că în fiecare regiune elementară densitatea este constantă și egală cu densitatea într-un anumit punct al acestei regiuni, adică. Apoi, produsul exprimă masa aproximativă a plăcii elementare, iar suma tuturor acestor produse este masa aproximativă a întregii plăci,
Valoarea exactă a masei întregii plăci se obține prin deplasarea la limita la, unde este cea mai mare dintre diametrele regiunii:
Ambele probleme au condus la necesitatea de a considera suma integrală bidimensională
pentru o funcție cu privire la un domeniu și limita acestuia pentru.
Definiția. Un număr este numit limita sumei integrale pentru dacă, pentru orice număr, există un număr astfel încât dacă
indiferent de alegerea punctelor din regiunile elementare.
Definiția. Un integrat dublu al unei funcții asupra unui domeniu este limita sumei sale integrale dacă există și nu depinde de metoda de partiționare a domeniului și de alegerea punctelor:
Aici funcția se numește integrand, iar domeniul se numește regiunea de integrare.
Integrul dublu al funcției în domeniu este de asemenea indicat după cum urmează:
Observăm fără o dovadă că limita sumelor integrale există dacă funcția este continuă într-un domeniu închis cu zonă. Dacă limita sumei integrale există, atunci funcția se numește integrabilă în domeniu. În consecință, toate funcțiile continue sunt integrabile, între funcțiile discontinue există funcții integrabile și neintegrabile.
Din soluția problemelor considerate mai sus, semnificația geometrică și fizică a integratului dublu urmează:
1. Semnificație geometrică: integrarea dublă a funcției r în regiune este egală cu volumul cilindrului cu baza, care este delimitat de sus de suprafața
2. Sensul fizic al integratului dublu: dacă o funcție non-negativă exprimă densitatea de suprafață a unei plăci, atunci masa sa este egală cu integralele duble ale unei funcții date pe o anumită regiune