Număr sisteme // Dmitri Tarasov [13:51]
Sistemul numerelor este un sistem de înregistrare a numerelor folosind numere. iar poziția numărului în număr determină greutatea și valoarea numerică.
Sistemul numeric este determinat complet de bază - numărul care determină numărul de cifre (începând cu numărul zero) din sistem, iar gradul (începând cu zero) este determinat de greutățile numerelor digitale (de la dreapta la stânga).
[edit] Exemple de sisteme de numere:
- binar (numere: 0-1);
- ternar (numere: 0-2);
- cuaternar (numere: 0-3);
- quinary (numere: 0-4);
- hexazecimal (numere: 0-5);
- septenar (numere: 0-6);
- octal (numere: 0-7);
- 9 cifre (numere: 0-8);
- zecimal (numere: 0-9);
- 11 cifre (numere: 0-9, A);
- duodecimal (figuri: 0-9, A-B);
- treisprezece (numere: 0-9, A-C);
- patru cifre (numere: 0-9, A-D);
- 15 cifre (numere: 0-9, A-E);
- hexazecimal (cifre: 0-9, A-F).
[edit] Algoritmi pentru traducerea numerelor:
Mai întâi, se face o secvență a numărului inițial și rezultatul (din diviziunile anterioare) privat (mai mare sau egal cu baza) la baza noului sistem de numere, iar restul diviziunilor sunt înregistrate. Diviziunea continuă până când privatul devine mai puțin decât pământul. Apoi, numerele din noul sistem de numere sunt scrise în loc de (obținute în sistemul de numere zecimale) din ultima divizie privată și restul diviziunilor în ordinea inversă (primire). Numărul rezultat este introducerea numărului original în noul sistem de numere.
[edit] Exemplu de traducere 10 → 2
Suma produselor din cifrele sistemului de numere originale (tradusă anterior în sistemul cu număr zecimal) se calculează în funcție de greutatea cifrelor (baza numărului de sistem în gradul numărului cifrei, începând cu zero) în sistemul original. Numărul rezultat este o înregistrare a numărului inițial în sistemul de numere zecimale.
[edit] Exemplul de traducere 2 → 10
Numărul inițial al sistemului binar este împărțit în perechi de cifre, începând cu numărul de unități (cel mai din dreapta). Ultima pereche poate fi incompletă, apoi se adaugă cifra 0 în partea stângă, apoi perechile de cifre sunt înlocuite cu numerele corespunzătoare (conform tabelelor perechilor) ale sistemului numeric cuaternar.
[edit] Tabelul de perechi
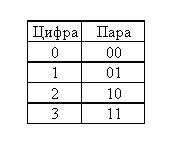
[edit] Exemplul de traducere 2 → 4
Numărul inițial al sistemului binar este împărțit în triade (triple de cifre ale sistemului binar) începând cu numărul de unități (cea mai dreaptă). Ultima triadă (cea mai stângă) poate fi incompletă, iar cifra 0 (una sau două) se adaugă la ea în stânga. Apoi, triadele sunt înlocuite cu cifrele corespunzătoare (conform tabelului triad) ale sistemului de numere octale.
[edit] Tabelul de triade
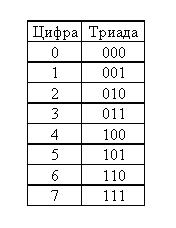
[edit] Exemplul de traducere 2 → 8
Numărul inițial al sistemului binar este împărțit în tetraduri (patru cifre ale sistemului binar) începând cu numărul de unități (cel din dreapta). Ultimul (tetradul din stânga) poate fi incomplet, apoi cifra 0 (una, două sau trei) este adăugată la stânga acestuia. Apoi tetradurile se înlocuiesc cu cifrele corespunzătoare (conform tabelului tetrad) ale sistemului numeric hexazecimal.
[edit] Tabelul tetradelor
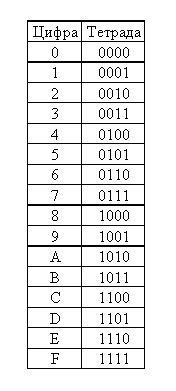
[edit] Exemplul de traducere 2 → 16
Cifrele numărului inițial al sistemului numeric cuaternar sunt înlocuite (de la stânga la dreapta) prin perechi de cifre ale sistemului de numere binare corespunzătoare (conform tabelului de perechi). Valoarea zero zero a primei perechi (stânga) este omisă (aruncată).
[edit] Tabelul de perechi

[edit] Exemplul de traducere 4 → 2
Cifrele numărului inițial al sistemului numerelor octale sunt înlocuite (de la stânga la dreapta) de triadele corespunzătoare (triade de cifre binare). Zero-urile non-zero ale primei triade (stânga) sunt omise (aruncate).
[edit] Tabelul de triade

[edit] Exemplul traducătorului 8 → 2
Cifrele numărului original al sistemului de numere hexazecimale sunt înlocuite (de la stânga la dreapta) cu tetradele corespunzătoare tetradului (conform tabelului tetrad) (patru cifre ale sistemului numeric binar). Zero-urile non-zero ale primului (stânga) tetrad sunt aruncate (aruncate).
[edit] Tabelul tetradelor
