Petri net de trei elemente: o mulțime de locuri, o mulțime de tranziții și o relație de incidență.
O simplă rețea Petri este un set de N = (S, T, F), unde- - O mulțime de locuri;
- - set de tranziții astfel încât.
- - Relația de incidență este astfel încât
(A);
(B)
Condițiile din clauza 3 indică faptul că pentru fiecare tranziție există un singur element care specifică un set multiplu de intrări pentru el și un multiset de ieșire. Să definim multiseturile de intrare și ieșire.
Multisitele de intrări și ieșiri de locuri și tranziții se găsesc din următoarele condiții:Lăsați rețeaua să fie dată.
- Dacă pentru o anumită tranziție avem, vom denota;
- .
Vom spune că acestea sunt de intrare. a - puncte de joncțiune ieșire. Astfel, conform definiției, este corect. Apoi vom spune că locul este incidental pentru tranziție dacă sau.
Extinzim funcțiile u la mai multe seturi de tranziții. Să existe o multitudine de tranziții astfel încât. Apoi am stabilit
Plasele Petri au o formă grafică convenabilă de reprezentare sub forma unui grafic, în care locurile sunt reprezentate de cercuri, iar tranzițiile sunt dreptunghiuri. Locații și tranziții, unde locul se alătură tranziției dacă se alătură cu dacă pentru un număr natural. Aici numărul este numit multiplicitatea arcului. care este reprezentat grafic lângă arc. Arcurile care au o multiplicitate a unităților vor fi notate fără a le atribui unul.
Un exemplu. Exemplu de rețea
În forma grafică, rețeaua este prezentată în Fig. Rețeaua are patru locuri și trei intersecții. Raportul stabilește arcul de rețea. Astfel, de exemplu, elementul specifică patru arce: de la θ și de la θ cu multiplicități 2, de la θ și de la multiplicități θ la unitate. Pentru că tranziția este corectă și. Pentru un loc, puteți calcula și.
Fig. 1: Exemplu de grafic Petri net
Conceptul de rețea în sine are un caracter static. Pentru a specifica caracteristicile dinamice, se utilizează conceptul de marcare a rețelei, adică funcție care atribuie un număr întreg fiecărui loc. Din punct de vedere grafic, marcajul este reprezentat sub formă de puncte numite jetoane și localizat în cercuri corespunzătoare locurilor din rețea. Absența etichetelor într-un anumit loc indică marcarea zero a acestui loc.
O etichetă Petri net este un set în care- - de rețea;
- - marcarea inițială.
Un exemplu. Un exemplu de rețea marcată.
Fig. 2: Exemplu de rețea Petri marcată
Plasele Petri au fost proiectate și utilizate pentru a simula sistemele paralele și asincrone. Când se modelează în plasele Petri, locurile simbolizează o anumită stare a sistemului, iar tranziția simbolizează unele acțiuni care au loc în sistem. Sistemul, fiind într-o anumită stare, poate genera anumite acțiuni, iar invers, executarea unor acțiuni întreprinde sistemul dintr-o stare în alta.
Starea actuală a sistemului determină marcarea rețelei Petri, adică localizarea etichetelor (jetoanelor) în locațiile din rețea. Executarea acțiunii în sistem, în rețelele Petri, este definită ca declanșarea tranzițiilor. Tranzițiile declanșatoare generează un nou marcaj, adică generează o nouă destinație de plasare a etichetelor (jetoanelor) în rețea. Definiți funcționarea rețelelor marcate, bazate pe funcționarea tranzițiilor individuale.
Regula de declanșare a tranzițiilor este următorul algoritmLăsați rețeaua să fie marcată.
- Se consideră că tranziția este activată (activată) atunci când etichetă, dacă;
- Tranziția excitată (activată) în timpul etichetei poate declanșa. conducând la un nou marcaj, care este calculat de regula :. Tranziția este indicată ca.
Cu alte cuvinte, tranziția este considerat a fi un excitat (activat), ca o etichetare în cazul în care fiecare site are intrare sale cel puțin numărul de etichete multitudine de arce corespunzătoare. Excitat (activat), tranziția se poate declanșa și la exploatarea fiecăruia dintre spațiul său de intrare este retrasă și se adaugă la fiecare intrare un număr de etichete multiplicitate egale de arce corespunzătoare. Dacă mai multe tranziții sunt activate simultan (activate), oricare dintre acestea sau orice combinație a acestora poate declanșa. De exemplu, permiteți tranzițiilor din și din rețea din Figura 2 să funcționeze. Obținem rețeaua prezentată în Figura 3.
Fig. 3: Noua rețea marcată.
O abordare compozițională a construcției rețelelor Petri sugerează posibilitatea construirii unor rețele mai complexe de componente mai puțin complexe. Pentru a face acest lucru, sunt introduse puncte de acces, care vă permit să combinați rețelele simple prin sincronizarea evenimentelor și a stărilor (tranziții și locuri).
Punctul de acces T este un punct definit de următoarele condiții
Lăsați rețeaua și o anumită alfabet să fie date. Un punct de acces T este un set unde
- - numele (identificatorul) punctului de acces t;
- - unele alfabete;
- - marcă funcție, unde. Notatia desemneaza setul de multiseturi finite si non-empty definite pe set.
Punctul de acces S este un punct definit de următoarele condiții
Lăsați rețeaua să fie dată. Apoi, punctul s-acces al N este un set, unde
- - numele (identificatorul) punctului de acces s;
- - setați astfel încât.
Conceptele introduse de puncte de acces oferă posibilitatea introducerii a două operațiuni de bază asupra rețelelor Petri pentru construirea rețelelor compozite:
1. Operațiunea de tranziție-îmbinare - permite generarea și descrierea sincronizării proceselor paralele (tmerge);
2. Funcționarea locurilor de îmbinare - vă permite să aplicați la operațiile de rețea compoziția, selecția, iterația secvențială și altele (smerg).
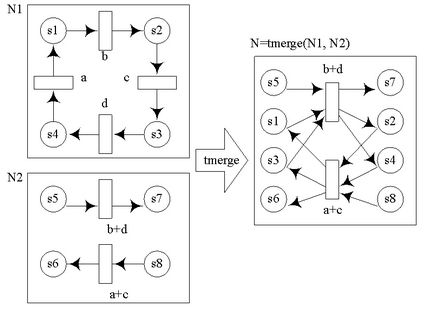
Fig. Figura 4: Exemplu de operațiune de tranziție de combinare
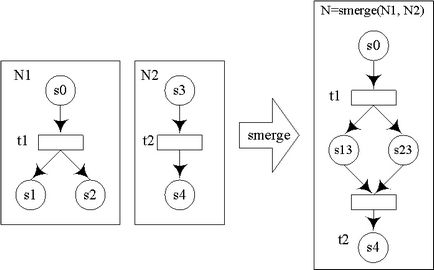
Fig. 5: Exemplu de operație de îmbinare
Operațiile de mai sus au următorul înțeles:
La îmbinarea locurilor - se definește setul de condiții dintr-o rețea care sunt identificați, fiind definită o condiție a rețelei definită de un nume de punct de acces s. Îmbinarea diferitelor rețele este realizată astfel încât, dacă starea descrisă este realizată într-o singură rețea, atunci această stare este obținută și pe cealaltă rețea;
La fuziunea tranzițiilor, se determină alfabetul evenimentelor vizibile din punctul de acces t. Fiecare tranziție la rețea este marcată fie de un eveniment invizibil, fie de o combinație de evenimente din alfabetul punctului de acces. Îmbinarea pe tranziții se face în așa fel încât dacă o anumită combinație de evenimente are loc atunci când o rețea este declanșată, atunci aceeași rețea de evenimente are loc în a doua rețea.
Știți că modelele sintetice sunt modele matematice concepute pentru a proiecta noi sisteme care diferă de sistemele cunoscute cu proprietăți specificate. Printre modelele economico-matematice sintetice se numără, de exemplu, modelele flotei mașinilor și a tractoarelor, modelele de formare a programelor de investiții etc.
ȘTIRI ALE FORUMULUI
Cavalerii teoriei eterului