Imaginea unui obiect în spațiu, construită pe un plan conform anumitor legi, se numește proiecția sa pe acest plan.
Proiecție centrală
Proiecția punctului A este (∙) A 'a intersecției liniei de proiectare cu planul α (figura 1).
Proiectia este procesul de construire a imaginilor cu ajutorul liniilor de proiectare
A '= AA'∩α, unde AA' este fasciculul proiectat
Proiecția unui punct pe un plan este punctul de intersecție al razei proeminente cu planul proiecțiilor.
Luăm în spațiu un obiect (în exemplul nostru, segmentul AB) și îl proiectăm din (•) S în planul α (figura 2).
Obținem proiecția segmentului AB pe planul α (A'B '). Dacă razele proeminente trec printr-un punct S. atunci această proiecție se numește proiecție centrală, S este centrul de proiecție. Această proiecție este folosită în pictura, arhitectură, fotografie.
Proiecție paralelă
Vom muta centrul de proiecție S în infinit, razele proeminente vor fi paralele între ele (figura 3).
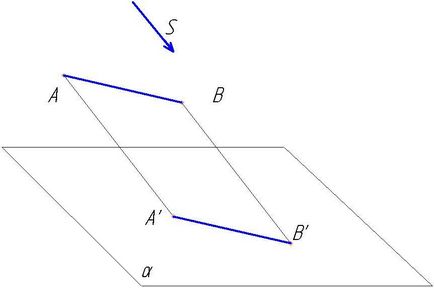
S - direcția de proiecție. O astfel de proiecție va fi numită paralelă. Razele proeminente sunt paralele.
În practica de inginerie, practic proiecție paralelă
În funcție de direcția razei proeminente față de planul proeminențelor, proeminențele paralele pot fi dreptunghiulare (figura 4);
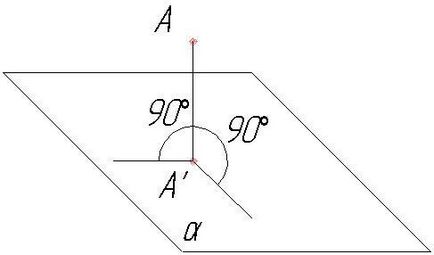
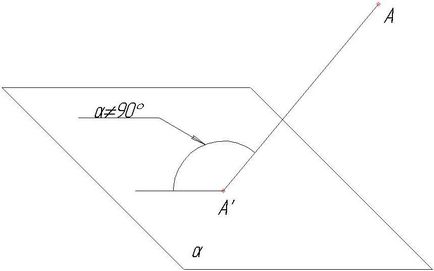
și unghiuri oblice (figura 5).
În viitor vom studia doar proiecțiile dreptunghiulare (ortogonale).
Proprietățile de bază ale proiecției paralele
În cazul proiecției paralele, caracteristicile metrice ale figurilor geometrice sunt încălcate (are loc o denaturare).
Rețineți principalele proprietăți ale proiecției paralele:
1. Proiecția unui punct este un punct.
2. Proiecția unei linii drepte pe un plan este o linie dreaptă.
3. Dacă în spațiu punctul aparține unei linii, atunci proiecția acestui punct aparține proiecției liniei.
4. Proiecțiile liniilor paralele sunt reciproc paralele, iar raportul dintre segmentele acestor linii este egal cu raportul dintre proiecțiile lor paralele.
5. Punctul de intersecție al proiecțiilor liniilor intersectate este proiecția punctului de intersecție al acestor linii în spațiu.
6. O figura dreaptă, plată, paralelă cu planul proiecțiilor, este proiectată pe acest plan cu o magnitudine reală.
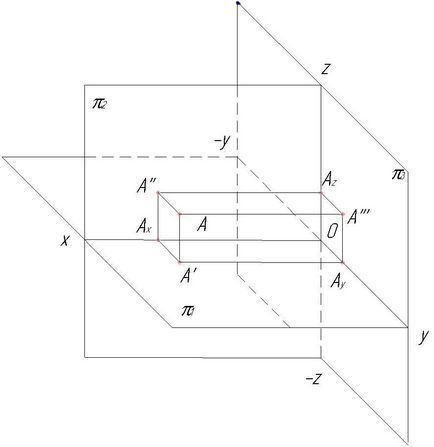
Metoda de proiecții ortogonale (metoda Monge).
π1 - planul orizontal al proiecțiilor
π2 - planul frontal al proiecțiilor
π3 este planul profilului proiecțiilor
În intersecția dintre planuri obținem axele coordonatelor x, y, z. Punctul de intersecție a coordonatelor se numește originea coordonatelor O sau a centrului proiecțiilor.
Din (•) A omitem ┴ prin 3 avioane și obținem proiecțiile unui punct pe aceste planuri:
A 'este proiecția orizontală (•) A
A "este proiecția frontală (•) A
A "este proiecția profilului (•) A
Distanțele de la (•) A la planurile de proiecție sunt denumite coordonatele punctului. Scara de-a lungul axelor Ox și Oz este de 1: 1, de-a lungul axei Oy - 1: 2. Pentru a determina poziția unui punct în spațiu, sunt necesare trei coordonate dreptunghiulare sau cele două proiecții ortogonale (Figura 6).
Se potrivește planul π1 cu π2 și π3 σπ2 prin rotirea în jurul axelor Ox și Oz, obținem o imagine netedă a punctului - diagrama. O astfel de imagine plat a punctului este prezentată în Fig.
La construirea (•) pe diagramă, proiecția orizontală a lui A 'este caracterizată de coordonatele x, y;
față A "- x, z;
profilul A "- y, z.
În diagrama orizontală și o vedere frontală (•), sunt pe de o ┴ la axa Ox (A'A „┴Ox). Frontală și proiecții de profil sunt pe același punct pe axa Oz ┴ (A“ A "„┴Oz). Inutil . acest desen plat, o denaturare a axelor Ox, Oy, Oz relație nici geometrică între trei proeminențe permite găsirea punctului a treia proeminență două dat grafic -. prin intermediul liniilor de proiecție și prin măsurarea coordonatelor.
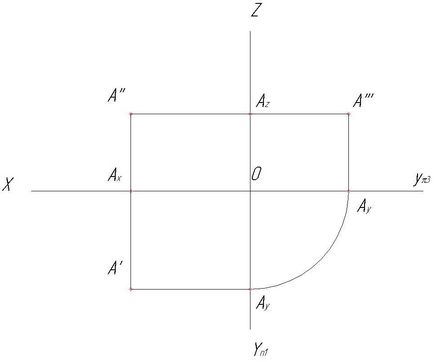
Exemplul 1. Pentru două proiecții date de punctele A, B, C, construiți oa treia. Construiți imagini vizuale ale punctelor (figura 8).
1. La intersecția liniei de comunicație A'A cu axa x, marchează axa auxiliară Ax (Figura 9).
2. Desenați o linie de comunicare de la proiecția orizontală a punctului A '
3. Transferăm punctul auxiliar Ay spre axa yp3. În acest scop, plasăm compasurile la originea (punctul O) a razei OAy și tragem arcul spre axa yp3.
4. Din proiecția frontală a punctului A "tragem o linie de comunicare
5. La intersecția liniilor de comunicare trase din punctele Ay și Az perpendiculare pe axele y și z. definim proiecția profilului punctului A '' '.
6. Pentru a găsi proiecția profilului B '' ', vom realiza liniile de comunicare
7. Pentru a construi proiecția C '' 'lipsă, argumentăm după cum urmează: C' (10,0); C "(10,0), unde z = 0 și y = 0, prin urmare, C" "(y, z) => C" (0,0) este la origine, în punctul O.
Construim imagini vizuale ale punctelor AV C (figura 10).
Axa y este direcționată la un unghi de 45 ° față de axa x. Când construim o imagine vizuală, luăm coeficientul de distorsiune de-a lungul axelor kx = kz = 1, ky = 0.5.
1. Notați punctele auxiliare Ax. Ay, Az. măsurarea distanțelor pe diagrama Monge.
3. Construim o imagine vizuală a punctului A.
(A '' A) || y (A '' 'A) | x. la intersecția acestor linii obținem punctul A.
Dacă punctul se află în spațiu, atunci pe diagrama nici una din proiecțiile sale cu punctul în sine nu coincide. Dacă una dintre coordonate este zero, punctul se află pe plan și coincide cu proiecția sa pe acest plan, atunci când două coordonate sunt zero, punctul se află pe axă. Când toate cele trei coordonate sunt egale cu zero, punctul se află la origine.