Forța. care acționează pe o particulă încărcată în mișcare într-un câmp magnetic, egală cu:
se numește forța Lorentz (forța magnetică).
Plecând de la definiția (1), modulul forței în cauză este:
unde este vectorul vitezei particulei, q este sarcina particulei, este vectorul inducției magnetice a câmpului în punctul de amplasare al încărcăturii și unghiul dintre vectori și. Din expresia (2) rezultă că, dacă încărcarea se deplasează paralel cu liniile de forță ale câmpului magnetic, atunci forța Lorentz este zero. Uneori forța Lorentz, încercând să izoleze, este desemnată folosind indexul:
Direcția forței Lorentz
Puterea lui Lorentz (ca orice forță) este un vector. direcția este perpendiculară pe vectorul viteză și vectorul (adică perpendicular pe planul în care sunt vectori de inducție magnetică și viteză) și regula dreaptă definite de regula (șurub dreapta) Fig.1 (a). Dacă avem de-a face cu o sarcină negativă, controlul tonului forței Lorentz este opus rezultatului produsului vectorial (figura 1 (b)).
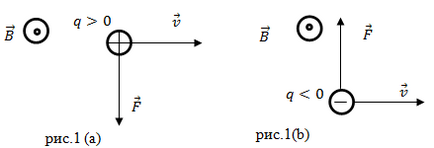
vectorul este direcționat perpendicular pe planul desenelor de pe noi.
Consecințele proprietăților forței Lorentz
Deoarece forța Lorentz este întotdeauna direcționată perpendicular pe direcția vitezei sarcinii, lucrarea ei asupra particulei este zero. Se pare că acțiunea pe o particulă încărcată cu un câmp magnetic constant nu-și poate schimba energia.
În cazul în care câmpul magnetic este o viteză uniformă și perpendiculară particulei încărcată, taxa sub influența forțelor Lorentz se vor deplasa raza R = circumferința const într-un plan care este perpendicular pe vectorul de inducție magnetică. Raza cercului este:
unde m - masa particulei, | q | - unitate de încărcare a particulelor, - Lorentz factor relativiști c - viteza luminii în vid.
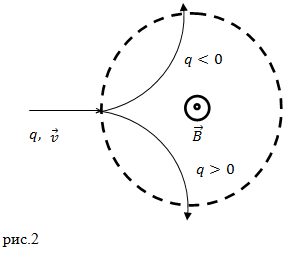
Puterea lui Lorentz este o forță centripetală. În direcția deviației particulei încărcate elementar într-un câmp magnetic, se face o concluzie cu privire la semnul său (figura 2).
Formula forței Lorentz în prezența câmpurilor magnetice și electrice
Dacă o particulă încărcată se deplasează într-un spațiu în care există simultan două câmpuri (magnetice și electrice), atunci forța care acționează asupra ei este egală cu:
unde este vectorul de intensitate a câmpului electric în punctul unde se află sarcina. Expresia (4) a fost obținută empiric de Lorentz. Forța care intră în formula (4) este numită și forța Lorentz (forța Lorentz). Divizarea forței Lorentz în componente: relativă electrică și magnetică, deoarece este asociată cu alegerea cadrului inerțial de referință. Deci, dacă cadrul de referință se mișcă la aceeași viteză ca și încărcătura, atunci într-un astfel de sistem forța Lorentz care acționează asupra particulei va fi zero.
Unități de măsură a forței Lorentz
Unitatea de bază de măsură a forței Lorentz (ca orice altă forță) în sistemul SI este: [F] = H
Exemple de rezolvare a problemelor
Sarcină. Care este viteza unghiulară a unui electron care se deplasează de-a lungul unui cerc într-un câmp magnetic cu inducția B?
Soluția. Deoarece un electron (o particulă având o încărcătură) se mișcă într-un câmp magnetic, atunci forța Lorentz acționează asupra ei:
unde q = qe este încărcarea electronică. Deoarece în stare se spune că electronul se mișcă de-a lungul unui cerc, aceasta înseamnă că, în consecință, expresia forței forței Lorentz va lua forma:
Forța Lorentz este centripetală și, în conformitate cu cea de-a doua lege a lui Newton, în cazul nostru va fi egală cu:
Ecuați laturile drepte ale expresiilor (1.2) și (1.3), avem:
Din expresia (1.3) obținem viteza:
Perioada de revoluție a electronului de-a lungul circumferinței poate fi găsită ca:
Cunoscând perioada, puteți găsi viteza unghiulară ca:
Sarcină. O particulă încărcată (sarcină q, masa m), la o rată de vvletaet o regiune în care intensitatea câmpului electric E și câmpul magnetic de inducție B. Vectori și aceeași direcție. Care este accelerația particulei în momentul inițierii deplasării în câmpuri, dacă?
Soluția. Să facem un desen.
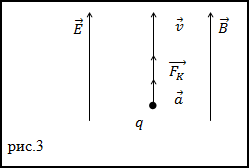
Partea încărcată este acționată de forța Lorentz:
Componenta magnetică are o direcție perpendiculară pe vectorul de viteză () și pe vectorul magnetic de inducție (). Componenta electrică este co-direcționată cu vectorul puterii () a câmpului electric. În conformitate cu noua lege a lui Newton, avem:
Obținem că accelerația este egală cu:
Dacă viteza de încărcare este paralelă cu vectorii și apoi. obținem: