Dependența liniară este exprimată prin formula y = ax + b. x este un argument, a și b sunt numere definite.
Dacă condițiile problemei nu limitează în nici un fel argumentul funcției liniare, se dovedește că domeniul funcției date este toate numerele reale. Pentru a găsi valoarea unei funcții liniare, trebuie să multiplicăm numărul a cu valoarea variabilei x. și apoi adăugați produsul rezultat cu numărul b. iar operațiile de multiplicare și de adăugare sunt întotdeauna fezabile. Condițiile problemei pot impune constrângeri suplimentare asupra argumentului.
Graficul unei funcții liniare este o linie dreaptă. Linia dreaptă este definită de 2 puncte. Deci, pentru a construi graficul unei funcții liniare, sunt plasate coordonatele a 2 astfel de puncte ale graficului, pentru a aplica punctele obținute pe planul de coordonate și prin ele pentru a trasa o linie dreaptă.
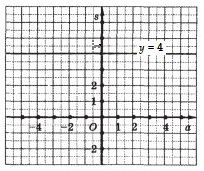
Să presupunem că numărul a este egal cu zero în formula y = ax + b. Atunci reprezentarea formală a funcției liniare ia forma
Funcția dată de formula y = b. pentru orice valoare a argumentului are aceeași valoare de b.
Să presupunem că numărul b este zero în formula y = ax + b. Atunci reprezentarea oficială a unei funcții liniare devine:
Funcția y = ax. unde x este argument și ≠ 0, aceasta este o proporționalitate directă.
Deoarece proporționalitatea directă este o funcție liniară, graficul direct proporțional este o linie dreaptă. Această linie aparține punctului (0; 0), deoarece dacă x = 0, atunci y = 0.
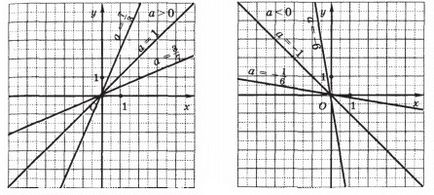
Pentru a construi rapid o proporționalitate directă, puteți găsi orice punct al graficului (nu (0; 0)) și trageți o linie dreaptă prin origine și punct găsit.
Graficele a două funcții liniare diferite ale formulei y = ax + b:
a) se intersectează. dacă coeficienții a sunt diferiți;
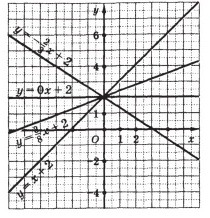
b) sunt paralele. dacă coeficienții a sunt aceiași.
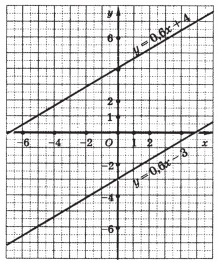
Prin proprietățile unei funcții liniare, pot fi rezolvate sistemele de ecuații liniare. Această soluție este elegantă, iar interpretarea grafică ajută la aprofundarea înțelesului conceptelor matematice.