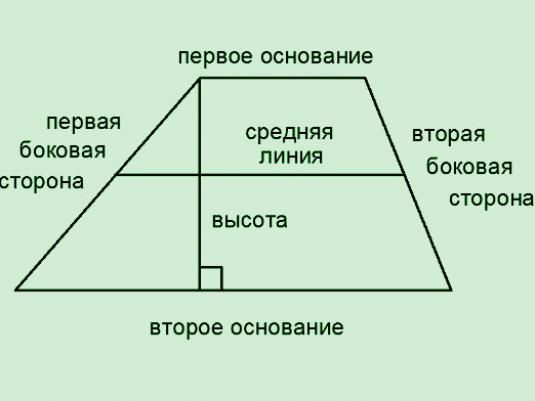
Un trapez este un patrulater, ale cărui două laturi sunt paralele (acestea sunt bazele trapezoidului, indicate în figurile a și b), iar celelalte două nu sunt (în figură, AD și CB). Înălțimea trapezoidului este segmentul h trasat perpendicular pe baze.
Cum să găsiți înălțimea trapezului pentru zonele trapezoidale cunoscute și lungimea bazei?
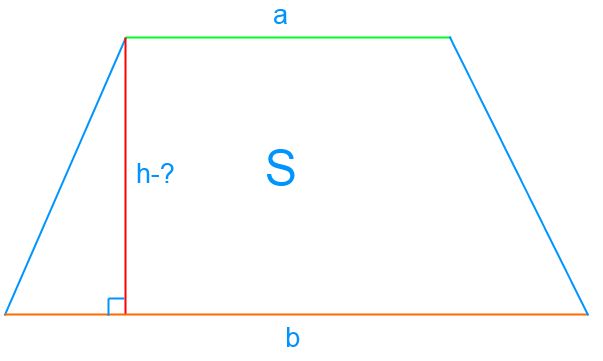
Pentru a calcula zona S a trapezoidului ABCD, se utilizează formula:
Aici segmentele a și b sunt bazele trapezoidului, h este înălțimea trapezului.
Dacă convertim această formulă, putem scrie:
Folosind această formulă, obținem valoarea h dacă zona S și lungimea bazelor a și b sunt cunoscute.
Dacă se știe că suprafața trapezoidului S este de 50 cmsup2, lungimea bazei a este de 4 cm, lungimea bazei b este de 6 cm, apoi pentru a găsi înălțimea h, folosim formula:
Înlocuiți cantitățile cunoscute în formulă.
h = (2 - 50) / (4 + 6) = 100/10 = 10 cm
Răspuns: Înălțimea trapezoidului este de 10 cm.
Cum pot găsi înălțimea unui trapez dacă se dau zona trapezoidală și lungimea liniei mediane?
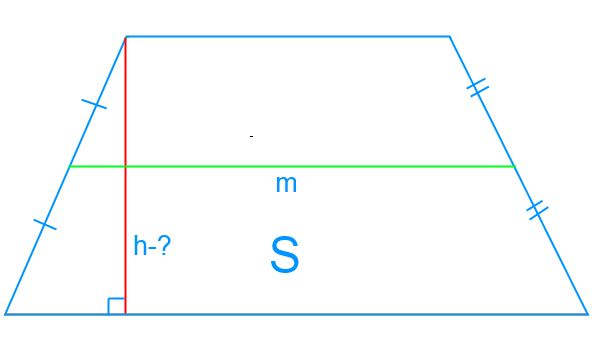
Utilizăm formula pentru calcularea suprafeței trapezoidului:
Aici m este linia de mijloc, h este înălțimea trapezului.
Dacă apare întrebarea, cum să găsiți înălțimea trapezoidului, formula:
h = S / m, va fi răspunsul.
Astfel, putem găsi înălțimea trapezului h, având valori cunoscute ale zonei S și segmentului liniei medii m.
Este cunoscută lungimea liniei medii a trapezului m, care este de 20 cm, iar suprafața S, care este egală cu 200 cmsup2. Să găsim valoarea înălțimii trapezului h.
Înlocuind valorile lui S și m, obținem:
h = 200/20 = 10 cm
Răspuns: Înălțimea trapezoidului este de 10 cm
Cum de a găsi înălțimea unui trapez dreptunghiular?
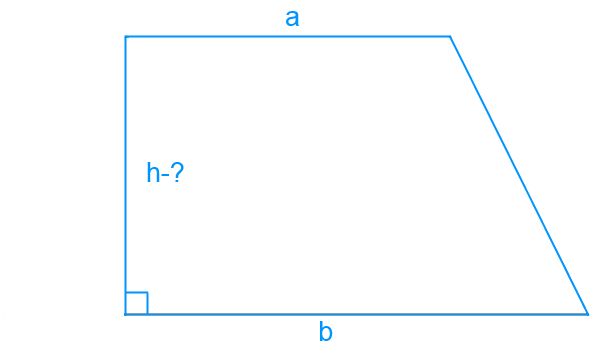
Dacă trapezoidul este un patrulater, cu două laturi paralele (baze) ale trapezoidului. Diagonala este un segment care conectează două vârfuri opuse ale unghiurilor trapezoidale (segmentul AC în figură). Dacă trapezoidul este dreptunghiular, folosind diagonala, găsim înălțimea trapezului h.
Un trapez dreptunghiular este un trapez astfel încât una din laturile laterale este perpendiculară pe baze. În acest caz, lungimea (AD) coincide cu înălțimea h.
Deci, ia în considerare trapezoidul rectangular ABCD, unde AD este înălțimea, DC este baza, AC este diagonala. Folosim teorema lui Pitagora. Pătratul hipotenentei AC a triunghiului dreptunghiular ADC este egal cu suma pătratelor picioarelor sale AB și BC.
Atunci putem scrie:
ACsup2- = ADsup2- + DCsup2-.
AD este cateterul triunghiului, partea laterală a trapezoidului și, în același timp, înălțimea acestuia. La urma urmei, segmentul AD este perpendicular pe baze. Lungimea sa va fi:
AD = radic- (ACsup2- - DCsup2-)
Deci, avem o formulă pentru calcularea înălțimii trapezului h = AD
Dacă lungimea bazei trapezoidului dreptunghiular (DC) este de 14 cm iar diagonala (AC) este de 15 cm, vom folosi teorema lui Pythagorean pentru a obține înălțimea (partea AD).
Fie x un picior necunoscut al unui triunghi drept (AD), atunci
ACsup2- = ADsup2- + DCsup2- pot fi scrise
15sup2- = 14sup2- + xsup2-,
x = radic- (15sup2--14sup2-) = radic- (225-196) = radic-29 cm
Răspuns: înălțimea trapezoidului dreptunghiular (AB) va fi radic-29 cm, care este de aproximativ 5.385 cm
Cum de a găsi înălțimea unui trapez isoscel?
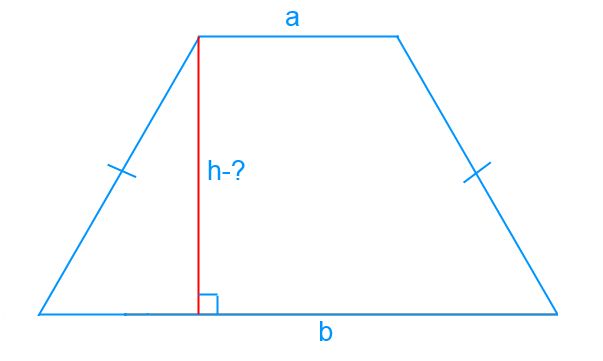
Un trapez izoscel este numit un trapez, în care lungimea laturilor laterale este egală una cu cealaltă. O linie dreaptă trasată prin mijlocul bazelor unui astfel de trapez va fi axa simetriei. Un caz special este trapezoidul, ale cărui diagonale sunt perpendiculare una pe alta, atunci înălțimea h, va fi egală cu jumătate din suma bazelor.
Să luăm în considerare cazul în cazul în care diagonalele nu sunt perpendiculare între ele. În trapezoidele echilaterale (isoscele), unghiurile de la baza și lungimea diagonalelor sunt egale. Este, de asemenea, cunoscut faptul că toate vârfurile unui trapez echilateral ating o linie de cerc trasă în jurul acestui trapez.
Luați în considerare desenul. ABCD este un trapez izoscel. Este cunoscut faptul că bazele trapezului sunt paralele, deci BC = b paralel cu AD = a, partea AB = CD = c, deci, unghiurile la baze sunt respectiv egale, putem scrie unghiul BAQ = CDS = alfa, și unghiul ABC = BCD = beta-. Astfel, concluzionăm că triunghiul ABQ este egal cu triunghiul SCD, deci segmentul
AQ = SD = (AD-BC) / 2 = (a-b) / 2.
Cu condiția problemei, valorile bazelor a și b și lungimea laturii c, găsim că înălțimea trapezului h este egală cu segmentul BQ.
Luați în considerare triunghiul drept ABQ. BO este înălțimea trapezului, perpendiculară pe baza AD și, prin urmare, pe segmentul AQ. Partea AQ a triunghiului ABQ, găsim, folosind formula derivată de la noi mai devreme:
Având valorile celor două picioare ale unui triunghi drept, găsim hypotenuse BQ = h. Folosim teorema lui Pitagora.
ABsup2- = AQsup2- + BQ²
Substituim datele de activitate:
csup2- = AQsup2- + hsup2-.
Obținem o formulă pentru găsirea înălțimii unui trapez izoscel:
Având la bază isoccele trapezoidale ABCD, unde baza AD = a = 10cm, baza BC = b = 4cm, iar partea AB = c = 12cm. În aceste condiții, să luăm în considerare, de exemplu, cum să găsim înălțimea trapezoidală, un trapez izoscel al unui ABCD.
Gasim partea AQ a triunghiului ABQ, înlocuind datele cunoscute:
AQ = (a-b) / 2 = (10-4) / 2 = 3 cm.
Acum înlocuiți valorile laturilor triunghiului cu formula teoremei pitagoreene.
h = radic- (csup2 - AQsup2-) = radic- (12sup2-3sup2-) = radicul-135 = 11,6 cm.
Răspuns. Înălțimea h a trapezoidului ABCD este de 11,6 cm.